Баланса. Модель Леонтьева

Запишем первую систему балансовых соотношений, характеризующих распределение продукции отраслей материального производства:

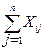+ y_i = X_i, i = .

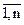Предположим, что межотраслевой поток продукции, идущей из i–й отрасли в j–ю, прямо пропорционален валовому выпуску той отрасли, куда они направляются, т.е.

X_ij = а_ij × X_j. (5.6)

Коэффициенты пропорциональности а_ij называются коэффициентами прямых материальных затрат и характеризуют количество продукции i–й отрасли, необходимой для выпуска единицы продукции j–й отрасли. Будем полагать, что коэффициенты а_ij постоянны в некотором промежутке времени, охватывающем как отчетный, так и предстоящий (планируемый) период.

Подставим выражение (5.6) в первое балансовое соотношение

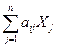+ y_i = X_i, i = 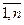. (5.7)

Выражение (5.7) называется системой уравнений межотраслевого баланса или экономико-математической моделью межотраслевого баланса, или моделью Леонтьева. Модель Леонтьева в матричном виде

АХ + Y = Х, (5.8)

где

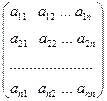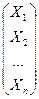А = , Х = , Y = .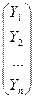

Можно сформулировать три типа задач межотраслевого баланса:

1. Известны коэффициенты прямых материальных затрат (а_ij; i,j = 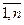) и объёмы конечного продукта всех отраслей у_i. Найти объёмы валового выпуска каждой отрасли X_i.

2. Известны объемы валового выпуска всех отраслей X_i и коэффициенты прямых материальных затрат а_ij. Найти объемы конечной продукции каждой отрасли y_i.

3. Известны коэффициенты прямых материальных затрат а_ij. Заданы объемы валового выпуска для части отраслей и объемы конечной продукции для всех остальных отраслей. Найти объемы конечной продукции для первых отраслей и объемы валового выпуска для вторых.