2015-01-30
4333
Для иллюстрации расчетов рассмотрим следующее графическое построение (рис. 38).
Ранний срок начала работы tPНij совпадает с ранним сроком свершения предшествующего работе события tPi:
tPНij = tPi. (3.7)
Поздний срок окрнчания работы tПОij совпадает с поздним сроком свершения последующего за работой события tПj:
tПОij = tПj. (3.8)
Ранний срок окончания работы tРОij:
tРОij = tРi + tij (3.9)
Поздний срок начала работы tПНij:
tПНij = tПj – tij. (3.10)
Полный резерв времени работы RПij показывает, насколько можно увеличить время выполнения данной работы или насколько можно передвинуть на более поздний срок начало работы, не изменяя окончательного срока выполнения комплекса работ:
RПij = tПj – tРi – tij. (3.11)
|
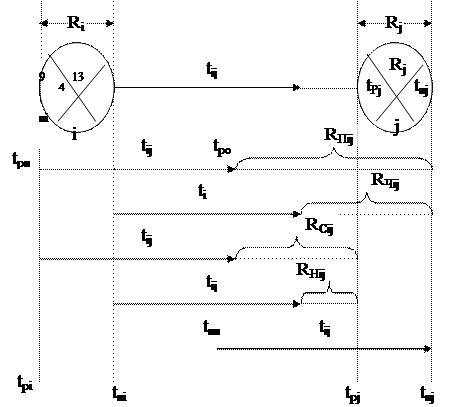
Рис. 38. Временные параметры работ и событий
Частный резерв времени работы (RЧij) – это часть полного резерва, на которую можно увеличить время завершения работы, уложившись в допустимо поздний срок ее окончания:
RЧij = tnj – tni – tij, RЧij = RПij – Ri. (3.12)
Свободный резерв времени работы RСij – это часть полного резерва, на которую можно увеличить время завершения работы, уложившись в ранний срок свершения ее последующего события:
RСij = tРj – tРi – tij, RСij = RПij – Rj. (3.13)
Независимый резерв времени работы RНij – это часть полного резерва, которая используется на увеличение продолжительности только данной работы, при этом все предшествующие работы могут заканчиваться в свои поздние сроки, а все последующие – в ранние:
RНij = tРj – tПi – tij, RНij = RПij – Ri – Rj. (3.14)
Использование независимого резерва не влияет на величину резерва времени других работ.
Частные случаи при расчете резервов:
1. Если на критическом пути лежит событие i, то из выражения (12) следует
Ri = 0; RПij = RЧij.
2. Если на критическом пути лежит событие j, то из выражения (14) следует
Rj = 0; RПij = RСij.
3. Если на критическом пути лежат и событие i и событие j, но сама работа не принадлежит критическому пути, то для этой работы все резервы равны
Ri = 0; Rj = 0; RПij = RЧij = RСij = RНij.
Коэффициент загруженности работы КЗ.
КЗ =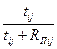 
. (3.15)
Результаты расчета временных параметров работ представлены в табл. 3.3.
Таблица 3.3
Временные параметры работ
| Код работы i - j | Длительность работы, tij | Сроки работы | Резервы времени | Коэф. загруженности, КЗ | ||||||
| tрн | tро | tпн | tпo | RП | RЧ | RС | RН | |||
| 1 – 2 | ||||||||||
| 2 – 3 | ||||||||||
| 2 – 4 | 0,5 | |||||||||
| 2 – 5 | 0,13 | |||||||||
| 3 – 5 | ||||||||||
| 3 – 6 | ||||||||||
| 4 – 6 | ||||||||||
| 4 – 9 | 0,26 | |||||||||
| 5 – 8 | 0,32 | |||||||||
| 6 – 7 | ||||||||||
| 7 – 8 | ||||||||||
| 8 – 9 | ||||||||||
| 9– 10 |
Для автоматизации расчёта параметров сетевой модели возможно использование программы «Расчёт и оптимизация сетевого графика» из ППП PRIMA. Для этого необходимо ввести коды работ в два смежных столбца Excel, ввести также длительности выполнения работ и количество необходимого ежедневно ресурса, например, трудового – требуемое количество исполнителей (рис. 39).
Результаты расчёта выводятся в табличной форме. Таблица временных параметров работ (рис._40) содержит информацию о кодах и продолжительности работ, а также расчётные значения полного и свободного резервов работ и коэффициента загрузки работ. Для работ критического пути коэффициент загрузки равен единице. Таблица временных параметров событий (рис. 41) включает расчётные значения ранних и поздних сроков свершения событий, а также резерва времени событий.
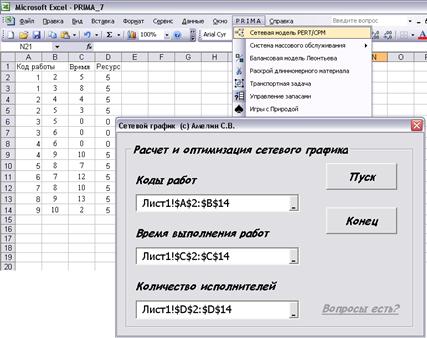
Рис. 39. Ввод исходных данных в диалоговую форму
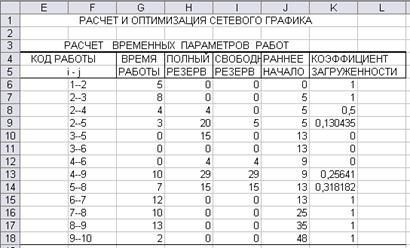
Рис. 40. Расчёт временных параметров работ
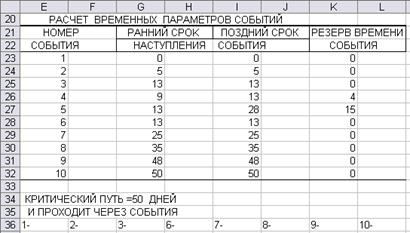
Рис. 41. Расчёт временных параметров событий
После таблиц выводится длительность критического пути и перечень событий, составляющих критический путь.
Оптимизация сетевого графика заключается в перераспределении исполнителей с менее загруженных работ на работы критического пути (если это возможно). Результатом оптимизации становится сокращение длительности критического пути (рис. 42).
При оптимизации сетевого графика используется следующая система уравнений
,
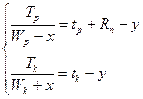где Тр – трудоёмкость работы, имеющей резерв времени; Тк – трудоёмкость работы критического пути; Wр – количество исполнителей работы, имеющей резерв; Wк – количество исполнителей работы критического пути; х – количество исполнителей, переводимых с работы, имеющей резерв на критический путь; tр – длительность работы, имеющей резерв времени; tк – длительность работы критического пути; у – время сокращения длительности критического пути и резерва времени работы; Rп – полный резерв времени работы.
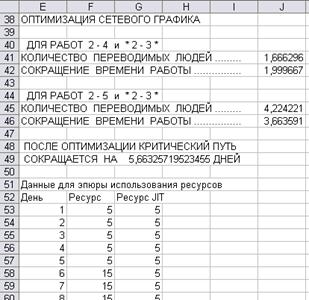
Рис. 42. Оптимизация сетевого графика и данные для
диаграммы использования ресурсов
Для построения календарного плана-графика выполнения работ – графика Ганта используется таблица временных параметров работ (рис. 43 - 49).
С помощью Мастера диаграмм на шаге 1 необходимо выбрать Линейчатую диаграмму с накоплением, которая позволяет строить горизонтальные отрезки. На шаге 2 указывается, что исходные данные содержатся в столбцах, после чего нужно переключиться на закладку Ряд. Далее следует Добавить Ряд 1, содержащий данные о ранних сроках начала работ, а в качестве Имени ввести слово: Обозначения. Ряд 2 содержит данные о продолжительности работ, а Ряд 3 – о полных резервах работ. На шаге 3 необходимо установить горизонтальные линии сетки, ввести название диаграммы – график Ганта и наименование осей – время и коды работ.
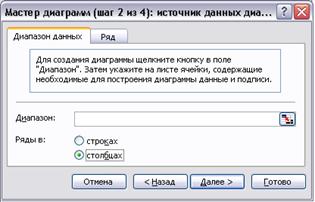
Рис. 43. Построение графика Ганта шаг 1 и шаг 2
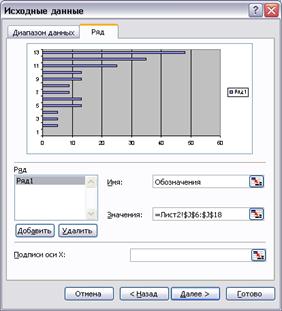
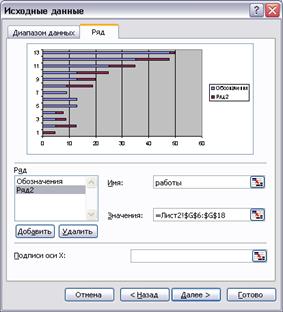
Рис. 44. Построение графика Ганта Ряд 1 и Ряд 2
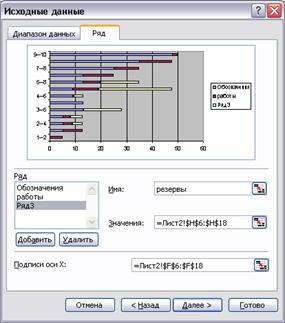
Рис. 45. Построение графика Ганта Ряд 3
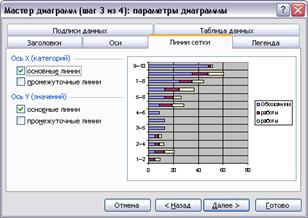
Рис. 46. Построение графика Ганта шаг 3 - Линии сетки
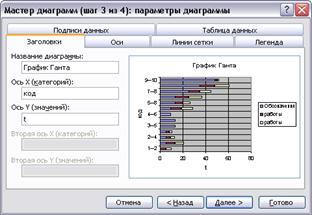
Рис. 47. Построение графика Ганта шаг 3 - Заголовки
После нажатия кнопки Готово получаем заготовку графика, которую ещё необходимо отформатировать. Далее, с помощью контекстного меню, вызываемого правой кнопкой мыши следует удалить серый фон диаграммы, установить требуемый размер шрифта надписей и цифр на шкалах, для вывода всех кодов работ установить Число категорий между подписями делений равным единице. Также следует установить Обратный порядок категорий для отображения графика Ганта ступенями сверху вниз.
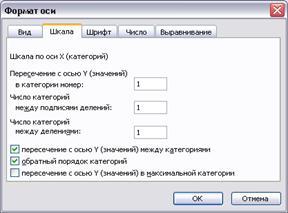
Рис. 48. Форматирование оси с кодами работ
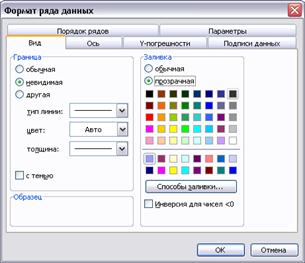
Рис. 49. Построение графика Ганта – удаление лишних линий
Для того чтобы сделать невидимыми синие горизонтальные полосы, соответствующие времени раннего начала работ, следует щелкнуть по любой из них правой кнопкой мыши и вызвать меню Формат рядов данных, в котором выбрать закладку Вид. Установить Границу – невидимую, а Заливку – прозрачную.
Для отображения фиктивных работ с нулевой длительностью можно искусственно установить для них после расчёта при построении диаграммы минимальную длительность, например, равную 0,3. Легенда диаграммы и подписи осей легко передвигаются с помощью мыши.
Диаграммы потребности в ресурсах (исполнителях) строятся на основе расчётных Данных для эпюры использования ресурсов. Если передвинуть время выполнения работ вправо за счёт имеющихся резервов, то можно сгладить пики потребности в ресурсах. Так, на первом графике (рис. 50), соответствующем ранним срокам начала работ, максимальное требуемое число исполнителей – 15, а если работы начинаются в возможно поздние сроки (just in time – JIT) – 10 человек (рис. 51).
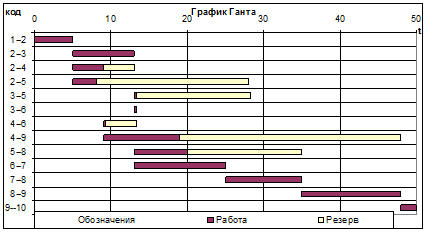
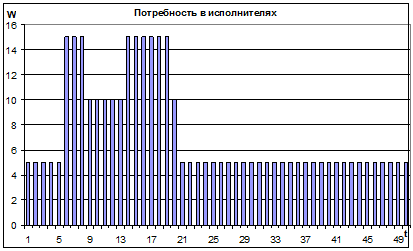
Рис. 50. График Ганта и диаграмма потребности в
ресурсах
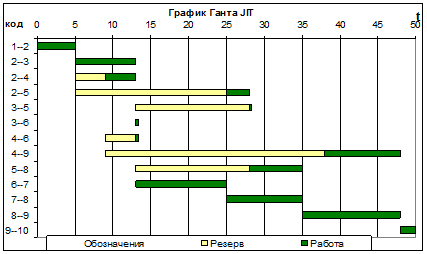
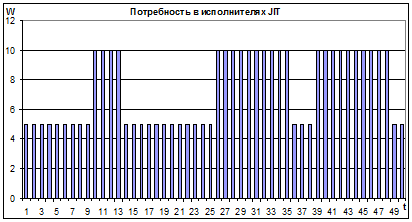
Рис. 51. График Ганта и диаграмма потребности в ресурсах JIT
Сетевое планирование в условиях неопределённости
В случаях, когда время выполнения работ точно не известно, то есть продолжительность работы является случайной (стохастической) величиной, характеризующейся законом β-распределения с числовыми характеристиками – средним значением, или математическим ожиданием продолжительности работы tож ij и дисперсией продолжительности работы σ2ij.
Для определения средней (ожидаемой) длительности работ на основе экспертного опроса даются три временные характеристики (оценки времени выполнения работ):
1. Оптимистическая (минимальная) оценка toij;
2. Пессимистическая (максимальная) оценка tnij;
3. Наиболее вероятная оценка tн.вij.
Тогда среднее (ожидаемое) время выполнения работы определяется выражением
toжij =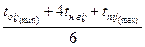 
,
или, если известны только крайние оценки:
toжij =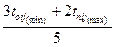 
.
Определение степени неопределённости выполнения работ, лежащих на критическом пути для первого подхода
,
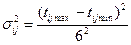для второго подхода
.
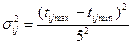Определение вероятности завершения комплекса работ в заданный директивный срок. Для этого необходимо найти аргумент функции нормального распределения Z по формуле
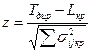
где Tдир – директивный срок завершения работ; Lкр – длительность критического пути; Sσ2ij кр – суммарная дисперсия работ, лежащих на критическом пути.
Максимальный срок выполнения всего комплекса работ Т при заданном уровне вероятности р
.
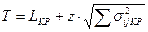Допустим, получены следующие оценки длительности работ (рис. 52), на основании которых рассчитано среднее (ожидаемые) время выполнения работ
tож 1-2 = (4 + 4 × 5 + 7) / 6 = 5,167.
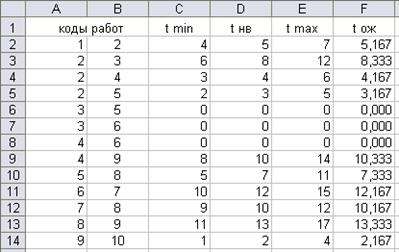
Рис. 52. Расчёт ожидаемой продолжительности работ
Длительность критического пути равна 51,3 дня. Для работ критического пути рассчитаем дисперсии
σ21-2= (7 – 4)2 / 62 = 0,25;
σ22-3= 1; σ26-7= 0,69; σ27-8= 0,25; σ28-9= 1; σ29-10= 0,25.
При расчёте с помощью программы «Расчёт и оптимизация сетевого графика» из ППП PRIMA, оценки времени выполнения работ tmin и tmax следует располагать в двух смежных столбцах, а для трёх оценок - значения tmin, tнв и tmax располагаются в трёх смежных столбцах, адреса которых вводятся в программу в окне Время выполнения работ.
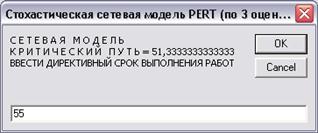
Рис. 53. Ввод директивного срока выполнения работ
Допустим, директивный срок выполнения работ установлен в пределах 55 дней (рис. 53), тогда аргумент функции нормального распределения равен
Z = (55–51,3) / (0,25+1+0,69+0,25+1+0,25)1/2 = 1,976.
Для определения вероятности завершения комплекса работ в заданный директивный срок используют значения функции нормального распределения Р(z):
| z | P(z) | z | P(z) | z | P(z) | z | P(z) |
| 0,0 | 0,50000 | 1,6 | 0,94520 | -3,0 | 0,00135 | -1,4 | 0,08076 |
| 0,2 | 0,57926 | 1,8 | 0,96407 | -2,8 | 0,00256 | -1,2 | 0,11507 |
| 0,4 | 0,65542 | 2,0 | 0,97725 | -2,6 | 0,00466 | -1,0 | 0,15866 |
| 0,6 | 0,72575 | 2,2 | 0,98610 | -2,4 | 0,00820 | -0,8 | 0,21186 |
| 0,8 | 0,78814 | 2,4 | 0,99180 | -2,2 | 0,01390 | -0,6 | 0,27425 |
| 1,0 | 0,84134 | 2,6 | 0,99534 | -2,0 | 0,02275 | -0,4 | 0,34458 |
| 1,2 | 0,88493 | 2,8 | 0,99744 | -1,8 | 0,03593 | -0,2 | 0,42074 |
| 1,4 | 0,91924 | 3,0 | 0,99865 | -1,6 | 0,05480 | 0,0 | 0,50000 |
Используя таблицу значений функции нормального распределения и метод интерполяции, определяют вероятность выполнения комплекса работ в заданный директивный срок.
Р(z) = 0,964+(1,976–1,8)×(0,977–0,964)/(2,0–1,8) = 0,976.
Для расчёта вероятности можно использовать функцию НОРМСТРАСП из категории Статистические Excel (рис. 54).
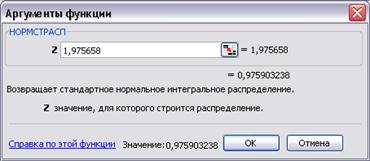
Рис. 54. Расчёт вероятности выполнения
всех работ в срок
Максимальный срок выполнения всего комплекса работ Т при заданном уровне вероятности р = 0,95. Для получения величины Z можно использовать функцию НОРМСТОБР из категории Статистические Excel (рис. 55).
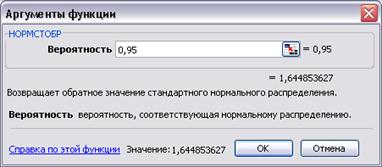
Рис. 55. Расчёт вероятного времени выполнения всех
работ
Т = 51,3+1,645× (0,25+1+0,69+0,25+1+0,25)1/2 ≈ 54,35 дня
Таким образом, с вероятностью 0,95 комплекс работ будет завершен за 54,35 дня.
Сформулируем сетевую модель как оптимизационную задачу линейного программирования. Поздний срок свершения завершающего события сетевого графика соответствует длительности самого продолжительного из полных путей - критического. Однако целью сетевого планирования является окончание комплекса работ в возможно короткие сроки. Отсюда целевая функция задачи линейного программирования заключается в нахождении минимального значения позднего срока завершающего события. В качестве ограничений задачи линейного программирования используем выражение для определения частного резерва времени работ. Тогда разность между поздними сроками свершения последующего события Tj и предшествующего события Ti, минус частный резерв времени работы Rчij будет равна продолжительности выполнения работы tij. Поздний срок свершения исходного события (как и его ранний срок свершения) равен нулю. Тогда математическая модель оптимизационной задачи сетевого планирования и управления будет иметь вид:
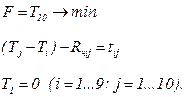
Введём исходные данные для расчёта в электронную таблицу Excel (рис. 56). Строку с адресами A2: W2 используем как область изменяемых ячеек для размещения искомых переменных (поздних сроков свершения событий и частных резервов времени работ). В соответствующие ячейки поля с адреса А4 по W16 вводим коэффициенты при переменных задачи с соответствующими знаками. Ячейка Х2 содержит целевую функцию (=J2), соответствующую позднему сроку свершения завершающего события. В ячейки Х4: Х16 введены выражения для левых частей ограничений. Так, ячейка Х4 содержит функцию (=СУММПРОИЗВ($A$2:$W$2; A4:W4), которая скопирована в ячейки Х5: Х16.
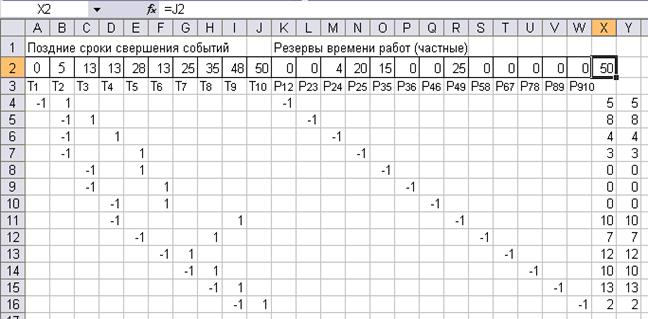
Рис. 56. Решение оптимизационной задачи сетевого планирования
Тема 4.ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
В результате изучения данной темы студенты должны:
знать:
- область применения моделей теории массового обслуживания в экономике;
- основные понятия теории массового обслуживания;
- методы решения задач теории массового обслуживания;
уметь:
- формулировать постановку различных задач теории массового обслуживания;
- находить решение задач теории массового обслуживания;
- давать экономическую интерпретацию полученных результатов решения задач теории массового обслуживания;
- применять методы теории массового обслуживания для решения практических задач;
владеть:
- математическим аппаратом теории массового обслуживания;
- практическими навыками формулирования и решения задач теории массового обслуживания, в том числе с помощью ЭВМ.
Основные понятия теории массового обслуживания. Предметом изучения теории массового обслуживания (ТМО) являются процессы, в которых, с одной стороны, возникают запросы на выполнение каких-либо работ или услуг, а с другой стороны – производится удовлетворение этих запросов. Такие процессы реализуются в системах массового обслуживания (СМО).
Та часть СМО, в которой возникают запросы, называется обслуживаемой подсистемой, а та часть СМО, которая принимает запросы и удовлетворяет их, называется обслуживающей подсистемой.
Каждый отдельный запрос на выполнение какой-либо работы называется заявкой,или требованием. Часть обслуживаемой подсистемы, которая в любой момент времени может послать только одно требование, называется источником требования, или объектом обслуживания. Обслуживанием называется удовлетворение поступившего в обслуживающую подсистему требования. Часть обслуживающей подсистемы, которая способна в любой заданный момент времени удовлетворять только одно требование, называется обслуживающим аппаратом. Обслуживающая подсистема – это совокупность однородных обслуживающих аппаратов (контролеров, наладчиков, рабочих, оборудования).
Прикладные задачи ТМО сводятся к тому, чтобы установить оптимальное соотношение между числом поступающих на обслуживание требований и числом обслуживающих устройств, при котором суммарные расходы на обслуживание и убытки от простоя были бы минимальными.
Поток требований – это последовательность возникающих во времени требований. Различают входящий и выходящий потоки и требований. По характеру потоки требований могут быть регулярными и стохастическими (вероятностными). В большинстве случаев входящий поток неуправляем и зависит от случайных факторов, т.е. и число требований, поступающих в систему в единицу времени, и интервал между требованиями – случайные величины.
Среднее число требований, поступающих в систему обслуживания в единицу времени, называется интенсивностью поступлений (l) и определяется по формуле
l =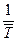 
, (4.1)
где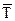 
- среднее значение интервала между поступлениями очередных требований.
СМО с простейшими потоками требований обладают следующими свойствами: стационарностью, ординарностью и отсутствием последействия.
Стационарным называется поток, характер которого с течением времени не меняется. При этом вероятность наступления того или иного числа событий за какой-либо промежуток времени зависит только от длины этого промежутка и не зависит от момента его начала.
Ординарным называется такой поток, в котором в любой момент времени может поступить не более одного требования.
Потоком без последействия называется поток, в котором вероятность поступления определенного числа требований после какого-то произвольного времени t не зависит от числа требований, поступивших в систему до этого момента времени.
Если поток требований простейший, то его можно описать количественно с помощью функции Пуассона:
Рк(t) =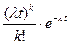 
, (4.2)
где Рk(t) – вероятность того, что в течение времени t в систему поступит точно k требований на обслуживание (k = 0,1,2 …).
Математически наличие простейшего потока требований можно определить с помощью статистической обработки данных. Одним из признаков закона распределения Пуассона является равенство математического ожидания случайной величины и ее дисперсии
lt = s2, (4.3)
где lt – среднее число требований, поступивших на обслуживание за время t.
Время обслуживания – это период, в течение которого удовлетворяется требование на обслуживание. Время нахождения требования в системе состоит из времени обслуживания и времени ожидания обслуживания. Время обслуживания одного требования – это случайная величина, характеризующаяся законом распределения, который определяется на основе статистических испытаний. На практике чаще всего исходят из гипотезы о показательном законе распределения времени обслуживания, в котором плотность распределения убывает с возрастанием времени.
При показательном законе распределения времени обслуживания функция распределения F(t)обсл, представляющая собой вероятность того, что время обслуживания будет меньше заданной величины t, описывается следующим образом:
F(t)обсл = 1 – е-nt, (4.4)
где n - параметр системы обслуживания, величина, обратная среднему времени обслуживания, представляет собой интенсивность обслуживания одного требования одним аппаратом:
n =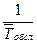 
, (4.5)
где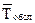 
- среднее время обслуживания одного требования одним аппаратом.
Параметр системы массового обслуживания a
a = 
, или a = l ×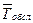 
. (4.6)
Параметр a показывает количество требований, поступающих в систему за среднее время обслуживания одного требования одним аппаратом. Поэтому количество обслуживающих аппаратов n не должно быть меньше a:
n ³ a. (4.7)
Если это требование не выполняется, то очередь будет расти и заявки не будут полностью выполнены.
