Пусть игра 2 х 2 имеет платежную матрицу (7.8). Изобразим на оси абсцисс отрезок горизонтальной линии единичной длины и обозначим концы отрезка через нуль и единицу. Из точек 0 и 1 по осям ординат восстановим перпендикулярные линии и изобразим на них выигрыши игрока А при использовании им соответственно чистых стратегий А1 и А2. Все промежуточные точки отрезка (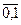 ) будут изображать смешанные стратегии:
) будут изображать смешанные стратегии:



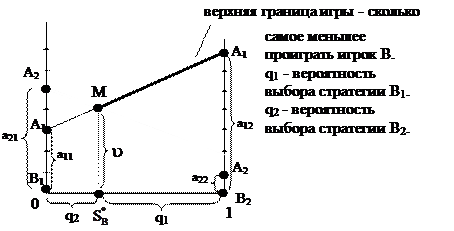
При оптимальной смешанной стратегии 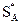 выигрыш игрока А будет составлять величину u и отмечен точкой М.
выигрыш игрока А будет составлять величину u и отмечен точкой М.
Произведем аналогичные построения для игрока В:


При графическом решении игр возможны и другие ситуации:
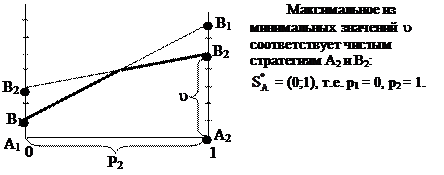
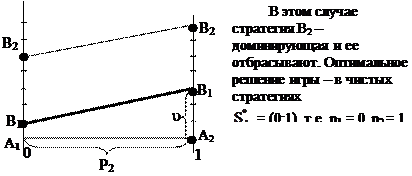 |
Пример. Найдем графическое и аналитическое решение игры:
| В1 | В2 | a = 4, b = 5, a ¹ b - следовательно, седловой точки нет. | |
| А1 | |||
| А2 |
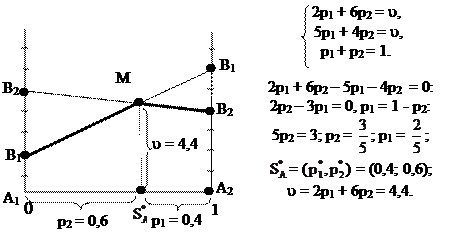 |
Найдем оптимальную смешанную стратегию игрока А
Найдем оптимальную смешанную стратегию игрока В:

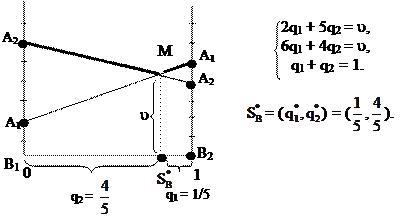
Игры 2 х n и m х 2
Допустим, платежная матрица задана и имеет вид 2 х n:
| В1 | В2 | … | Вn | Игрок А имеет две стратегии, а игрок В – неограниченное число стратегий. | |
| А1 | a11 | a12 | … | a1n | |
| А2 | a21 | a22 | … | a2n |
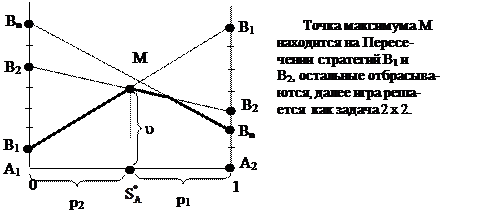
Допустим, платежная матрица имеет вид m х 2:
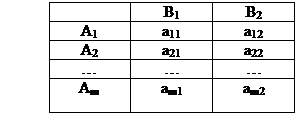 |
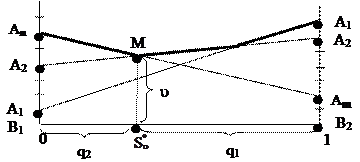
Минимум М находится на пересечении стратегий А1 и Аm, остальные отбрасываются, далее игра решается как задача 2 х 2.
Пример. Пусть игра задана в виде платежной матрицы
| В1 | В2 | В3 | Игра (2 х 3) не имеет седловой точки a = 4, b = 5, a ¹ b, имеем игру в смешанных стратегиях. | |
| А1 | ||||
| А2 |
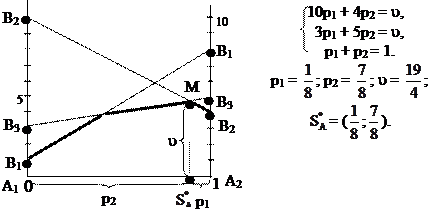 |
Решим задачу графически и аналитически. Для игрока А: получаем игру 2 х 2, используя стратегии В2 и В3 игрока В:
Для игрока В:
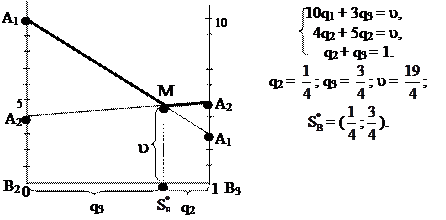
 2015-01-30
2015-01-30 729
729








