Игра два на два (2 х 2)

Рассмотрим игру, в которой у игроков А и В по две стратегии. Платежная матрица имеет вид

	В1	В2	(7.8)
А1	a11	a12
А2	a21	a22

Рассмотрим случай, когда игра не имеет седловой точки.

Теорема 4. Пусть 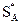и 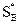– оптимальные смешанные стратегии игры с платежной матрицей (7.1) и ценой игры u, тогда для любого i, при котором выполняется строгое неравенство

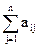q_j < u,

имеет место равенство p_i = 0. А если p_i > 0, то

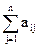q_j = u.

Аналогично, если для некоторых j

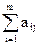× p_i > u,

то для этих j q_j = 0. А если q_j > 0, то

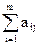× p_i = u.

Определим оптимальную смешанную стратегию 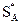игрока А, а для этого решим систему трех уравнений с тремя неизвестными

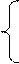а₁₁ × p₁ + а₂₁ × p₂ = u,

а₁₂ × p₁ + а₂₂ × p₂ = u,

p₁ + p₂ = 1.

Решив следующую систему, найдем оптимальную стратегию 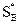игрока В:

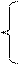а₁₁ × q₁ + а₁₂ × q₂ = u,

а₂₁ × q₁ + а₂₂ × q₂ = u,

q₁ + q₂ = 1.

Рассмотрим первую систему. Вычитая из первого равенства второе, получая

(а₁₁ - а₁₂) × p₁ + (а₂₁ - а₂₂) × p₂ = 0.

Подставим P₂ = 1 – P₁, тогда

(а₁₁ – а₁₂) × p₁ + (а₂₁ – а₂₂) (1– p₁ ) = 0,

отсюда оптимальная смешанная стратегия для игрока А – S*(p₁, p₂)

это – хорошо

P₁ = (а₂₂ – а₂₁)/(а₁₁ – а₁₂ + а₂₂ – а₂₁),

P₂ = 1– P₁ = (а₁₁ – а₁₂)/(а₁₁ – а₁₂ + а₂₂ – а₂₁).

цена игры

u = (а₁₁ × а₂₂ – а₂₁ × а₁₂)/(а₁₁ – а₁₂ + а₂₂ – а₂₁).

Рассуждая аналогично, для определения оптимальной стратегии игрока В получая

q₁ = (а₂₂ – а₁₂)/(а₁₁ – а₁₂ + а₂₂ – а₂₁),

q₂ = (а₁₁ – а₂₁)/(а₁₁ – а₁₂ + а₂₂ – а₂₁).

Пример. Имеются две конкурирующие фирмы А и В, выпускающие изделия двух модификаций. Изучение спроса покупателей показало, что если выпускаются изделия первой модификации обеими фирмами, А₁ и В₁, то 40 % покупателей предпочитают изделия фирмы А и 60 % - фирмы В. Если выпускаются изделия А₁ и В₂, то 90 % покупателей приобретают изделия А. Если изготавливаются изделия А₂ и В₁, будет продано 70 % изделий фирмы А. Наконец, если выпускаются изделия второй модификации А₂ и В₂ обеими фирмами, то 20 % покупателей предпочитают изделия фирмы А.

Решение. Представим выигрыш фирмы А в табличной форме

а₁₁ = 40 % - 60 % = -20 %; а₁₂ = 90 % - 10 % = 80 %;

а₂₁ = 70 % - 30 % = 40 %; а₂₂ = 20 % - 80 % = -60 %.

	В1	В2	ai
А1	-20		-20
А2		-60	-60
bj

Нижняя цена игры составляет (-20), верхняя равна 40. Игра не имеет седловой точки. Найдем оптимальные смешанные стратегии

p₁ = (-60 - 40)/(-20 –80-60-40) = 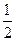; p₂ = ;

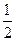u = [-20 × (-60)- 40 × 80]/ (-20 –80-60-40) = 10;

q₁ = (-60 - 80)/(-20 –80-60-40) = 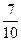; q₂ = .

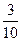Выигрыш фирмы А в соответствии с ценой игры составит 10 %. Следовательно, предпочтение покупателей можно выразить как А – В = 10 %, но А + В = 100 %, тогда А = 55 %; В = 45 %. Следовательно, при таких оптимальных стратегиях изделия фирмы А будут покупать 55 % потребителей, а фирма В – 45 % потребителей.