Решение игры в смешанных стратегиях

Теорема 3. Для того чтобы смешанные стратеги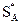и и 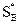были оптимальными в игре с матрицей (7.1) и ценой игры u, необходимо и достаточно, чтобы выполнялись следующие неравенства:

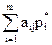³ u; j = 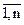, причем 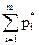= 1; (7.3)

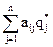£ u; i = 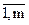, причем 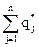= 1. (7.4)

Нахождение оптимальной стратегии можно свести к решению задачи линейного программирования.

Пусть требуется найти оптимальные стратегии для игры с заданной платежной матрицей (7.1), для которой a_ij строго больше нуля (а_ij >0, i= 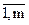,j = 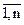), тогда цена игры u > 0. Найдем оптимальную стратегию игрока А – ().

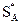Разделим левую и правую части в выражении (7.3) на положительную величину u:

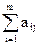
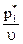³ 1; = .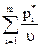

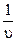Введем обозначение 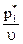= Х_i, тогда

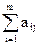Х_i ³ 1; j = ; = .

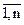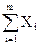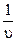Поскольку игрок А стремится сделать свой гарантированный выигрыш (u) как можно большим (u ® max), то величина 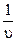должна быть как можно меньше (u ® min), тогда имеем следующую задачу линейного программирования:

f(x) = 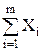® min, (7.5)

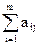Х_i ³ 1; j = 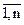, (7.6)

Х_i ³ 0; i = 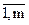. (7.7)

Если Х* = (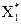, ,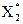… … 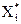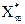) – оптимальный план задачи (7.5) – (7.7), а минимум функции f(x) = f(x*) = f*, то цена игры u при этом составит u = 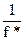, а т.к. 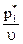= Х_i, тогда 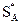= (u × 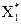,… u × 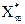) = (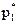,… 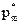) – оптимальная смешанная стратегия игрока А.

Для игрока В используя выражение (7.4), получим

g(y) = 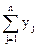® max.

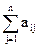y_j £ 1, i = .

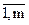y_j ³ 0; j = .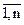

Решение игры u = ;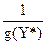

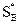= (u × 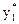,… u × ) = (,… ).

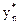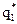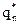Пример. Найти оптимальные смешанные стратегии игры, заданной следующей платежной матрицей:

	В₁	В₂	В₃	нижняя цена игры a = 4, верхняя цена игры b = 5, т.е. a ¹ b – седловой точки нет.
А₁
А₂

Сведем данную задачу к задаче линейного программирования.

Найдем оптимальную стратегию игрока А – ():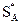

f(x) = X₁ + X₂ ® min.

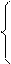X₁ + 8X₂³ 1,

10X₁ + 4X₂³ 1,

3X₁ + 5X₂³ 1,

X₁, X₂³ 0.

f(x) = 0,21; X₁= 0,026; X₂= 0,184,

отсюда

u = 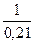= 4,76; P₁= 4,76 × 0,026 = 0,124;

P₂= 4,76 × 0,184 = 0,876.

Найдем оптимальную стратегию игрока В – ():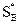

g(y) = y₁ + y₂ + y₃® max.

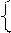y₁ + 10y₂+ 3y₃£ 1,

8y₁ + 4y₂+ 5y₃£ 1,

y₁, y₂, y₃³ 0.

g(y) = 0,21; y₁= 0; y₂= 0,0526; y₃ = 0,158,

отсюда

q₁ = 0; q₂= 4,76 × 0,0526 = 0,25;

q₃= 4,76 × 0,158 = 0,75.

Таким образом, применяя свою первую чистую стратегию с вероятностью 0,124 и вторую – с вероятностью 0,876, игрок А выигрывает величину 4,76. Игрок В, применяя свою вторую чистую стратегию с вероятностью 0,25 и третью – с вероятностью 0,75, проигрывает величину 4,76, иначе он проигрывает больше.