2015-01-30
473
Рис. 2.21. Тонкостенная труба под действием внутреннего
давления, продольной силы и крутящего момента
|
Рассматривается цилиндрическая труба наружным радиусом R, толщиной стенки d (рис. 2.21). Отношение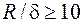 
. Отношение длины l к радиусу 
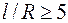. Труба нагружена внутренним давлением 
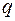, по ее торцам приложены силы 
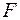и крутящие моменты 
.
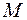Напряжения в трубе обозначаем, используя местную декартову систему координат x, y, z: ось x параллельна оси трубы, ось z направлена по касательной к срединной линии поперечного сечения, осью y служит продолжение радиуса R.
Сила 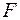вызывает в поперечном сечении трубы продольное усилие 
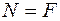и создает нормальное напряжение (рис. 2.22)
.
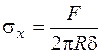Рис. 2.23. Напряжения в трубе
от внутреннего давления
|
Здесь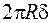 
– площадь поперечного сечения тонкостенной трубы.
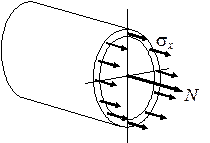Рис. 2.22. Напряжения
в трубе от продольной силы
|
Внутреннее давление вызывает растяжение трубы в кольцевом направлении (рис. 2.23), чему соответствует напряжение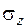 
в продольных сечениях трубы:
.
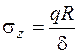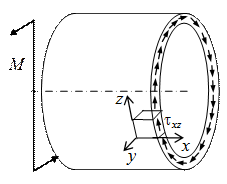Рис. 2.24. Напряжения
в трубе от крутящего
момента
|
Напряжения 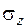положительны при 
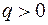. Случай 
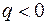отвечает давлению, приложенному к наружной поверхности.
Крутящий момент создает касательные напряжения (рис. 2.24):
.
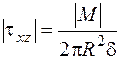Они направлены так, чтобы уравновесить пару сил М.
По толщине трубы напряжения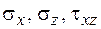 
распределены равномерно. Остальные напряжения либо в точности равны нулю, либо малы: 
, 
.
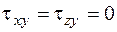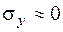Напряженное состояние элементарного параллелепипеда, вырезанного из трубы (рис. 2.25), является плоским. Анализ напряженного состояния выполняется так же, как в задаче № 7.
