2015-01-30
1018
Расчет допусков выполняет конструктор изделия на этапе проектирования. Для расчета допусков необходимо иметь уравнение погрешностей, устанавливающее взаимосвязь погрешностей выходных параметров с погрешностями деталей и элементов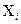 
, входящих в него. В общем случае все процессы делятся на детерминированные (функциональные), когда у разработчика имеется формула (аналитическое выражение, связывающее выходной параметр с входными), этот вариант рассмотрен в настоящем параграфе, и стохастические(вероятностные), которые будут рассмотрены в дальнейшем изложении. Покажем решение этого вопроса в случае, когда известна функциональная зависимость между выходными и входными параметрами.
Выходной параметр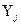 
представляет собой функцию многих переменных: линейных размеров деталей, их физические свойства, параметров источников питания и т.д., соединяемых при сборке, т.е.
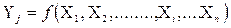(1.11)
где n-количество переменных.
В реальных условиях 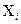имеют отклонения, которые находятся в пределах поля допуска, на входные, первичные параметры 
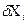.Обычно величины этих отклонений 
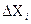от номинала 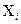невелики (редко, когда 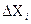достигают 30%),что позволяет использовать линейную модель и используя формулу полного дифференциала выражения (1.11) перейти к конечным приращениям:
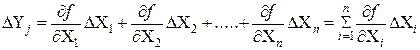(1.12)
Здесь погрешности являются размерными величинами; на практике при суммировании погрешностей различной физической природы (сопротивлений, индуктивностей, давлений и т.д.) удобнее пользоваться относительными, безразмерными величинами. Разделив (1.12) на (1.11) получим:
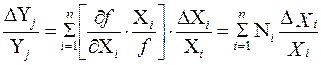(1.13)
Часть уравнения (1.13) в квадратных скобках называется коэффициентом влияния N и определяет степень влияния погрешностей деталей на погрешность выходного параметра Yj.
Перейдем от абсолютных отклонений к относительным и введем обозначения ∆Y\Y =δY; ∆X\X =δX. Тогда уравнение (1.13) можно записать в виде:
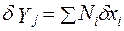(1.14)
