 .
.
До сих пор мы говорили о разложении в тригонометрический ряд функции, заданной на отрезке 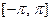 . Рассмотрим теперь случай, когда
. Рассмотрим теперь случай, когда 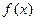 задана лишь на части
задана лишь на части 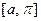 этого отрезка, где
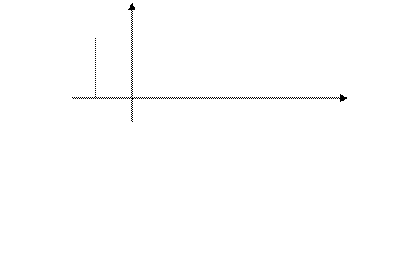
этого отрезка, где 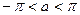 (рис. 4) Будем предполагать
(рис. 4) Будем предполагать 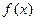 дифференцируемой на этом отрезке, и поставим вопрос о построении такого тригонометрического ряда
дифференцируемой на этом отрезке, и поставим вопрос о построении такого тригонометрического ряда
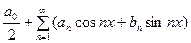 , (3)
, (3)
в который разлагалась бы функция 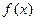 .
.
 |

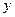
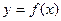
а 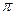

Рис. 4
Эту задачу можно решить так: выберем совсем произвольную функцию 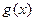 , заданную и дифференцируемую на отрезке
, заданную и дифференцируемую на отрезке 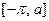 и определим на всём отрезке
и определим на всём отрезке 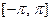 «составную» функцию
«составную» функцию 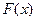 , положив
, положив
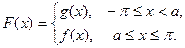
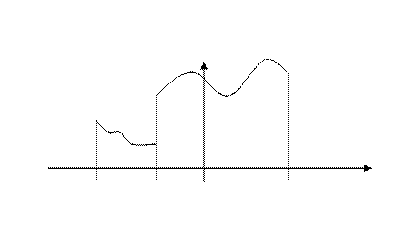
График 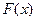 изображён на рис. 5.
изображён на рис. 5.
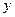
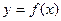
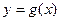
- 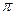 а
а 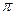

Рис. 5
Функция 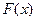 разлагается в свой ряд Фурье на всём отрезке
разлагается в свой ряд Фурье на всём отрезке 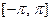 , за исключением может быть трёх точек
, за исключением может быть трёх точек 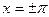 и
и 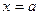 . В этих точках сумма ряда будет соответственно равна
. В этих точках сумма ряда будет соответственно равна
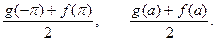
Поскольку, при 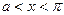 «составная функция
«составная функция 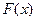 совпадает с
совпадает с 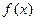 , то для этих х будет
, то для этих х будет
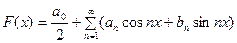 .
.
Если подбирать 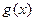 с условием
с условием 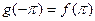 , то окажется
, то окажется 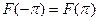 и равенство будет верно и при
и равенство будет верно и при 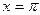 . Нако- нец, условие
. Нако- нец, условие  обеспечит справедливость равенства и при
обеспечит справедливость равенства и при 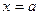
Таким образом, поставленная задача имеет решение. Однако это решение не единственно: ведь функцию 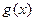 мы могли выбирать бесконечным множеством способов, а выбор этой функции определяет коэффициенты ряда.
мы могли выбирать бесконечным множеством способов, а выбор этой функции определяет коэффициенты ряда.
Например, 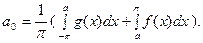
Поэтому (в отличие от функции, заданной на всём отрезке 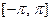 ) функция, заданная на более коротком отрезке, допускает бесконечное множество представлений вида (3). Здесь не имеет место теорема о единственности.
) функция, заданная на более коротком отрезке, допускает бесконечное множество представлений вида (3). Здесь не имеет место теорема о единственности.
Всё сказанное о 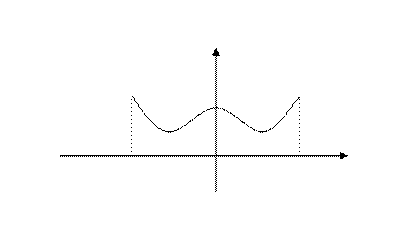 тносится, в частности, и к отрезку
тносится, в частности, и к отрезку 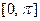 . Но тут появляется некое новое обстоятельство. Именно, если мы захотим, взять
. Но тут появляется некое новое обстоятельство. Именно, если мы захотим, взять 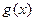 такой, чтобы «составная функция»
такой, чтобы «составная функция» 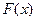 оказалась чётной (рис. 9).
оказалась чётной (рис. 9).
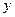
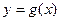
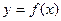
 О
О 

Рис. 6
Это приводит к разложению
 , (4)
, (4)
в котором
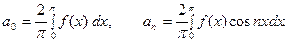 . (5)
. (5)
Нетрудно видеть, что формула (4) верна на всём отрезке 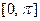 .
.
С другой стороны, мы можем выбрать 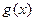 и так, чтобы функция
и так, чтобы функция 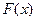 оказалась нечётной (рис. 7). Это приведёт нас к разложению
оказалась нечётной (рис. 7). Это приведёт нас к разложению
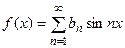 , (6)
, (6)
в котором
 . (7)
. (7)

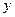
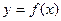
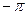 О
О 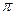

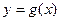
Рис. 7
Формула (6) верна при 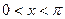 . Чтобы она была верна при
. Чтобы она была верна при 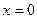 , необходимо, чтобы было
, необходимо, чтобы было 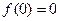 , так как правая часть равенства (6) обращается в ноль при
, так как правая часть равенства (6) обращается в ноль при 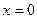 . Точно также для справедливости формулы (6) в точке
. Точно также для справедливости формулы (6) в точке 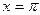 необходимо, чтобы было
необходимо, чтобы было 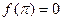 .
.
Таким образом, имеет место.
ТЕОРЕМА 1. Функцию 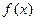 , заданную и дифференцируе - мую на отрезке
, заданную и дифференцируе - мую на отрезке 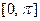 можно бесконечным множеством спо- собов разложить в тригонометрический ряд. В частности, её можно разложить по косинусам в ряд (4), коэффициенты которого определяются формулами (5), или в ряд по синусам (6) с коэффициентами (7).
можно бесконечным множеством спо- собов разложить в тригонометрический ряд. В частности, её можно разложить по косинусам в ряд (4), коэффициенты которого определяются формулами (5), или в ряд по синусам (6) с коэффициентами (7).
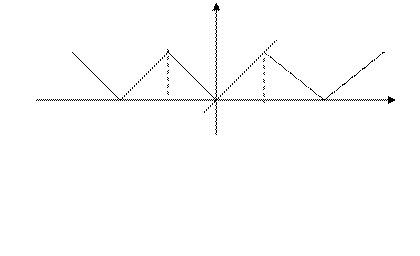
ПРИМЕРЫ. 1). Пусть 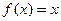 . Разложить эту функцию в ряд по косинусам
. Разложить эту функцию в ряд по косинусам
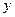
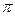
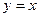
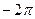
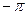 О
О 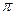
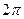

Рис. 8
Здесь
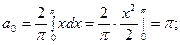
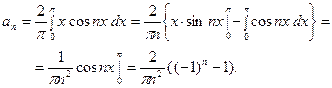
Отсюда, при 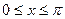 будет
будет
 (8)
(8)
В частности, при 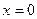 мы снова находим
мы снова находим
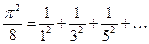
Сумма ряда (8) является 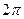 - периодической и чётной функцией. Её график изображён на рис. 8.
- периодической и чётной функцией. Её график изображён на рис. 8.
2). Пусть функция 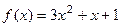 , заданная на
, заданная на 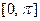 , разложена в тригонометрический ряд по синусам. Найти сумму ряда
, разложена в тригонометрический ряд по синусам. Найти сумму ряда 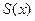 в точках
в точках
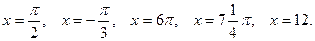
Решение. а) Так как  то
то
 Так как
Так как 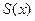 нечётная, то
нечётная, то
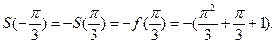 с)
с) 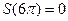 ,
,
так как при  все члены ряда обращаются в ноль
все члены ряда обращаются в ноль 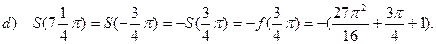
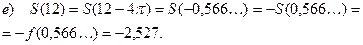
Сдвиг основного промежутка.
Всю теорию рядов Фурье мы излагали для функций, заданных на отрезке 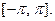 Однако вместо этого отрезка можно было бы положить в основу любой другой отрезок длины
Однако вместо этого отрезка можно было бы положить в основу любой другой отрезок длины 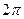 . Дело в том, что это период всех функций сис- темы:
. Дело в том, что это период всех функций сис- темы:
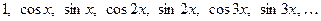 (9) и справедлива
(9) и справедлива
ТЕОРЕМА 2. Если функция 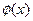 имеет период равный
имеет период равный 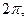 то интеграл
то интеграл 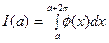 не зависит от числа а.
не зависит от числа а.
В самом деле,
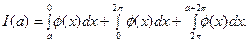 (10)
(10)
В последнем интеграле справа можно сделать замену 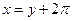 , дающую
, дающую
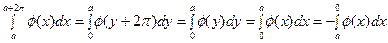
Таким образом, первый и третий интегралы правой части (10) взаимно уничтожаются и
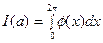 ,
,
чем и доказана теорема.
В частности, из неё следует, что 1) любые две функции системы (9) взаимно ортогональны на всяком отрезке длины 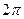 и 2) при всяком
и 2) при всяком 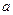 будет
будет
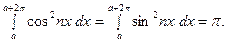
Следовательно, всю теорию можно перенести с отрезка 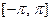 на любой отрезок
на любой отрезок 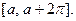 Например, верна:
Например, верна:
ТЕОРЕМА 3. Если функция 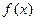 дифференцируема на от- резке
дифференцируема на от- резке 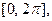 то всюду на открытом промежутке
то всюду на открытом промежутке 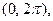 будет
будет
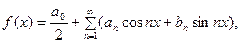 (11)
(11)
где
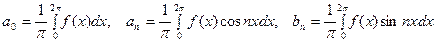
Ряд (11) сходится и в точках 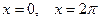 , где его сум -ма равна
, где его сум -ма равна
 .
.
ПРИМЕР. Разложить в ряд Фурье функцию 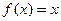 , рассматриваемую на отрезке
, рассматриваемую на отрезке 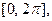
Здесь
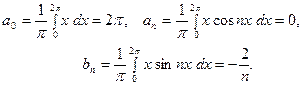
Следовательно, при 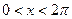 будет
будет
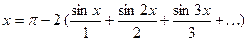 . (12)
. (12)
В частности, при 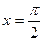 получаем уже знакомое равенство
получаем уже знакомое равенство

В точках 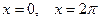 сумма
сумма 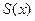 ряда (12) равна
ряда (12) равна 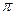 .
.
Нетрудно понять, что 
§ 4. РЯД ФУРЬЕ ДЛЯ ФУНКЦИИ С ПРОИЗВОЛЬНЫМ
ПЕРИОДОМ.
Мы видели, что ряды вида
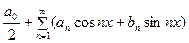 (1)
(1)
являются хорошим аналитическим аппаратом для представ- ления функций, заданных на промежутке длины 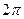 .
.
Рассмотрим теперь функции 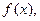 заданные на отрезке длины
заданные на отрезке длины 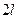 . Пусть для определённости речь идёт о функции
. Пусть для определённости речь идёт о функции 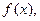 заданной и дифференцируемой на отрезке
заданной и дифференцируемой на отрезке  По- ложим
По- ложим
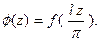
Тогда 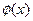 будет заданной и дифференцируемой уже на отрезке
будет заданной и дифференцируемой уже на отрезке 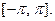 Значит, к
Значит, к 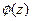 применима теория, изложен -ная выше, и потому при
применима теория, изложен -ная выше, и потому при 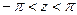 будет
будет
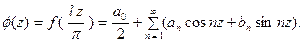
Положим в этом равенстве 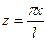 .
.
Тогда для 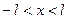 получаем равенство
получаем равенство
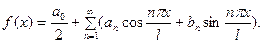 . (2)
. (2)
В точках 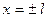 сумма ряда равна
сумма ряда равна
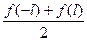 .
.
Остановимся на коэффициентах ряда (2). Например,
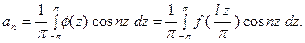 .
.
Подстановка 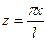 даёт
даёт
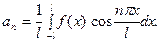
Аналогично,
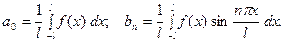
Что касается функций, заданных и дифференцируемых на отрезке 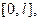 то они допускают бесчисленное множество разложений вида (2). В частности, их можно разлагать по косинусам и по синусам. Последнее разложение имеет вид
то они допускают бесчисленное множество разложений вида (2). В частности, их можно разлагать по косинусам и по синусам. Последнее разложение имеет вид
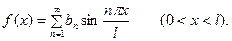 ,
,
где
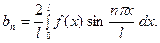 (3)
(3)
ПРИМЕРЫ.
1. Найти разложение в ряд Фурье функции:
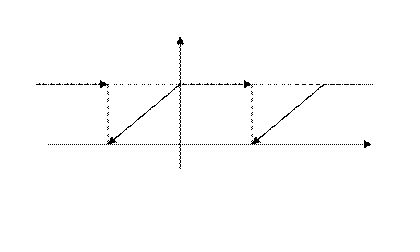
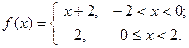

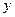
-2 0 2  Рис. 9
Рис. 9
Найдём коэффициенты Фурье. 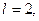 тогда
тогда
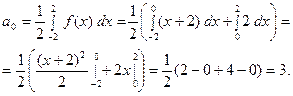
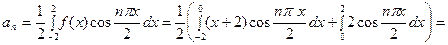 Для первого интеграла применим формулу интегрирования по частям;
Для первого интеграла применим формулу интегрирования по частям;
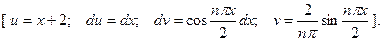
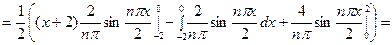

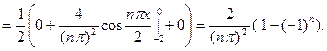
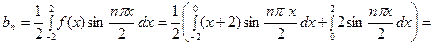 Для первого интеграла применим формулу интегрирования
Для первого интеграла применим формулу интегрирования
по частям;

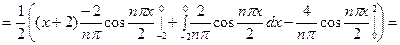

Следовательно, на промежутке 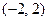 ряд Фурье имеет вид
ряд Фурье имеет вид
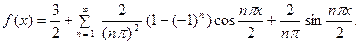
2. Найти ряд Фурье для чётной функции:
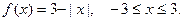

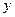
-3 0 3 6 
Рис. 10
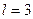 , функция чётная, поэтому
, функция чётная, поэтому 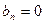 . Найдём остальные коэффициенты ряда, учитывая, что при
. Найдём остальные коэффициенты ряда, учитывая, что при 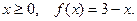

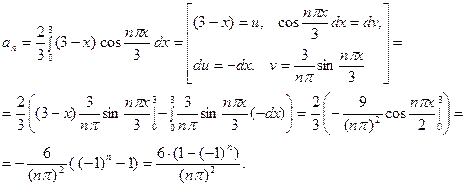 Тогда получаем:
Тогда получаем:
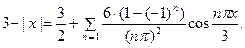
3. Разложить функцию 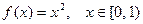 в неполный ряд Фурье по
в неполный ряд Фурье по 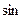 .
.
Дополним график функции нечётным образом.
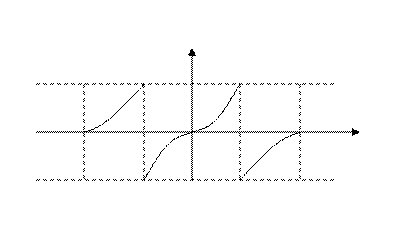
-2 -1 0 1 2 
-1
Рис. 11
В данном примере 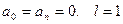 . Коэффициенты
. Коэффициенты 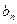
находим по формуле:
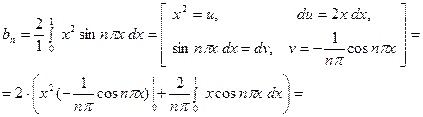
Второй интеграл снова интегрируем по частям:

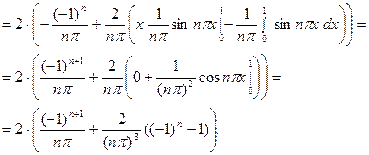
Тогда: 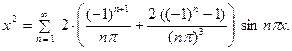
§ 5 РЯД ФУРЬЕ В КОМПЛЕКСНОЙ ФОРМЕ.
Пусть дан ряд Фурье для функции 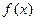 на отрезке
на отрезке 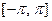 :
:
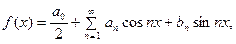 (1) с коэффициентами
(1) с коэффициентами
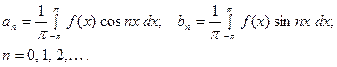 (2)
(2)
Обратимся к формуле Эйлера:
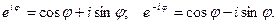
Отсюда
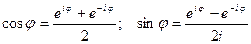 . (3)
. (3)
Используя формулы (3), получаем;
 .
.
Подставим данные выражения в ряд (1)

Полученный ряд и является рядом Фурье в комплексной форме. При этом коэффициенты данного ряда вычисляются по формулам:
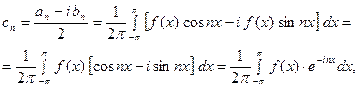
аналогично,
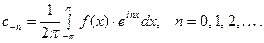
Такие же формулы можно получить, преобразовав ряд Фурье для случая произвольного промежутка 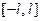 :
:
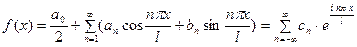 , (4) где
, (4) где
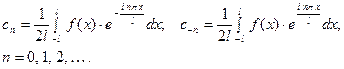
Или 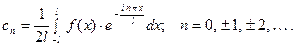
Очевидно, что ряд Фурье в комплексной форме имеет более компактный вид.
В электротехнике и радиотехнике элементы ряда Фурье в комплексной форме
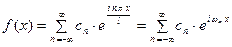
называются гармониками, коэффициенты 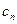 - комплексными амплитудами,
- комплексными амплитудами, 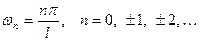 - волновыми числами функции
- волновыми числами функции 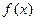 .
.
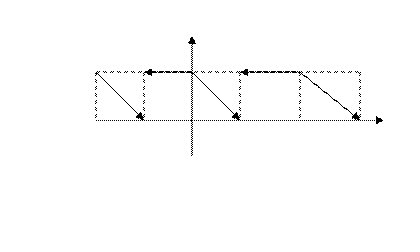
ПРИМЕР. Построить ряд Фурье в комплексной форме для функции:
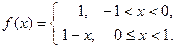
Для данной функции 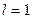 .
.
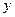
-2 -1 0 1 2 3 
Рис. 12
При 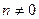 ,
,
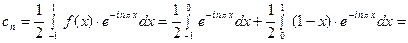
для второго интеграла
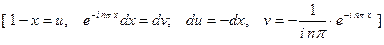
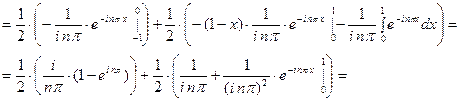
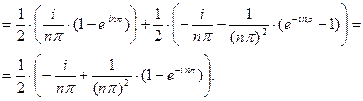
При 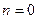

Следовательно, для всех точек непрерывности функции 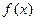 имеет место равенство:
имеет место равенство:
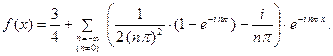
§ 6. ПРИЛОЖЕНИЯ РЯДОВ ФУРЬЕ.
 2015-01-30
2015-01-30 1169
1169








