Событие A – по крайней мере два шара одноцветные.
Противоположное событие:
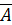 – все шара разного цвета.
– все шара разного цвета.
Рассмотрим события:
A 1 = бчк – первый шар белый, второй шар черный, третий шар красный.
Аналогично:
A 2 = бкч; A 3 = чбк; A 4 = чкб; A 5 = кбч; A 6 = кчб.
Событие A произойдет, если произойдет любое из событий A 1, A 2, A 3, A 4, A 5, A 6:
A = A 1 + A 2 + A 3 + A 4 + A 5 + A 6.
Так как шары в урну не возвращают, то при вычислении вероятности события A 1 = бчк рассчитываем условные вероятности того, что второй шар черный (при условии, что первый шар белый) и что третий шар красный (при условии, что первый шар белый и второй шар черный):
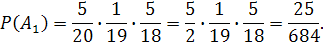
Аналогично:
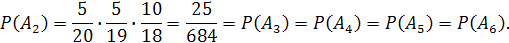
По теореме сложения вероятностей для несовместных событий:
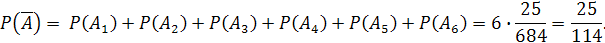
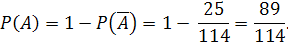
Ответ: 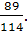
 2015-01-30
2015-01-30 448
448








