График функции (вероятностная гистограмма)

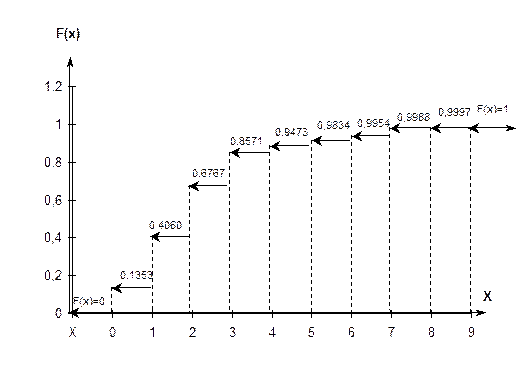
Рис. 4.6.

г) Определим вероятность того, что в течение 15 минут в банк прибудут хотя бы два инкассатора.

“Хотя бы два” - “как минимум два” - “два или больше”. Другими словами, “хотя бы два” - это “или два, или три, или четыре, или...”.

Исходя из этого, для определения вероятности того, что в течение 15 минут в банк прибудут хотя бы два инкассатора, можно использовать теорему сложения вероятностей несовместных событий:

P(X 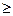2) = P(X = 2) + P(X = 3) + P(X = 4) +... + Р(Х = n).

С другой стороны, все возможные значения случайной величины образуют полную группу событий, а сумма их вероятностей равна 1. По отношению к событию (Х ³ 2) до полной группы событий не хватает события (Х < 2), т. е. (х 1), которое является противоположным событию (Х ³ 2). Поэтому искомую вероятность того, что в течение 15 минут в банк прибудут на автомобиле хотя бы два инкассатора, проще найти следующим образом:

P(X ³ 2) = 1 - P(X £ 1) = 1 - (P(X = 0) + P(X=1)) = 1 - (0,1353 + 0,2707) = 1 - 0,406 =

= 0,594.

Вероятность того, что в течение 15 минут в банк прибудут на автомобиле хотя бы два инкассатора, составляет 0,5904.

д) Определим вероятность того, что в течение 15 минут число прибывших инкассатор окажется меньше трех.

“Меньше трех” - это “или ноль, или один, или два”.

Из теоремы сложения вероятностей несовместных событий следует:

P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2).

P(X < 3) = 0,1353 + 0,2707 + 0,2707 = 0,6767.

Ответ. Вероятность того, что в течение 15 минут в банк прибудет меньше трех инкассаторов, составляет 0,6767.

Пример 4.3. Из 20 лотерейных билетов выигрышными являются 4. Наудачу извлекаются 4 билета.

а) Составьте ряд распределения числа выигрышных билетов среди отобранных;

б) Найдите числовые характеристики этого распределения;

в) Напишите функцию распределения числа выигрышных билетов среди отобранных и постройте ее график;

г) Определите вероятность того, что среди отобранных 4 билетов окажется не меньше трех выигрышных билетов;

д) Определите вероятность того, что среди отобранных 4 билетов окажется не больше одного выигрышного билета.

Решение. В качестве случайной величины в данной задаче выступает число выигрышных билетов среди отобранных. Обозначим ее через X.

Перечислим все возможные значения случайной величины Х: 0, 1, 2, 3, 4.

Это - дискретная случайная величина, т.к. ее возможные значения отличаются друг от друга не менее чем на 1, и множество ее возможных значений является счетным.

Очевидно, что отбор лотерейных билетов - бесповторный. Следовательно, испытания - зависимые.

Вышеперечисленные признаки указывают на то, что рассматриваемая случайная величина - число выигрышных билетов среди отобранных - подчиняется гипергеометрическому закону распределения.

Изобразим ситуацию на схеме:

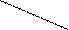N

M N-M

n

m n-m

Рис. 4.7.

Случайная величина, интересующая нас, Х = m - число выигрышных билетов в выборке объемом в n билетов. Число всех возможных случаев отбора n билетов из общего числа N билетов равно числу сочетаний из N по n (С ), а число случаев отбора m выигрышных билетов из общего числа M выигрышных билетов (и значит, (n-m) проигрышных из общего числа (N - M) проигрышных) равно произведению

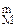С × С 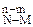(отбор каждого из m выигрышных билетов может сочетаться с отбором любого из (n-m) проигрышных). Событие, вероятность которого мы хотим определить, состоит в том, что в выборке из n лотерейных билетов окажется ровно m выигрышных. По формуле для расчета вероятности события в классической модели вероятность получения в выборке m выигрышных билетов (то есть вероятность того, что случайная величина Х примет значение m) равна:

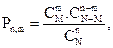
где С - общее число всех единственно возможных, равновозможных и несовместных исходов,

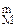С × С 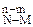- число исходов, благоприятствующих наступлению интересующего нас события;

m £ n, если n £ M и m £ M, если M < n.

Если по этой формуле вычислить вероятности для всех возможных значений m и поместить их в таблицу, то получим ряд распределения.

а) Составим ряд распределения.

Вычислим вероятности того, что случайная величина примет каждое из своих возможных значений и запишем полученные результаты в таблицу.

По условию задачи N =20; M = 4; n = 4; m = 0, 1, 2, 3, 4.

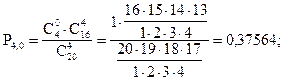
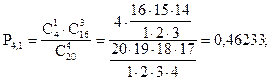
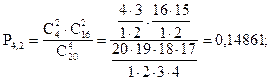
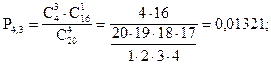
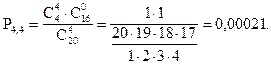
Занесем полученные результаты в таблицу:

Таблица 4.7.

X
P(X)	0,37564	0,46233	0,14861	0,01321	0,00021

Произведем проверку. Так как все возможные значения случайной величины образуют полную группу событий, сумма их вероятностей должна быть равна 1.

Проверка: 0,37564 + 0,46233 + 0,14861 + 0,01321 + 0,00021 = 1.

График полученного распределения вероятностей дискретной случайной величины - полигон распределения вероятностей; изображенный на рис 4.8

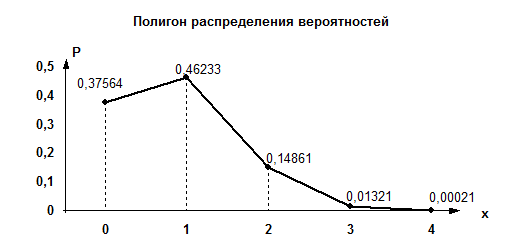
Рис. 4.8.

б) Найдем основные числовые характеристики распределения данной случайной величины.

Можно рассчитать математическое ожидание, дисперсию и среднее квадратическое отклонение по общим для любой дискретной случайной величины формулам.

Но математическое ожидание случайной величины, подчиняющейся гипергеометрическому распределению, может быть рассчитано по более простой формуле:

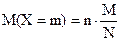Рассчитаем математическое ожидание числа выигрышных билетов среди отобранных:

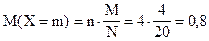(билета).

Дисперсию случайной величины, подчиняющейся распределению, также может быть рассчитано по более простой формуле:

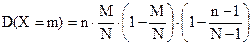Вычислим дисперсию числа выигрышных билетов среди отобранных:

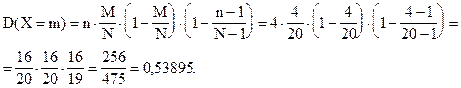
D(X = m) = 0,53895 (кв.ед.).

Рассчитаем среднее квадратическое отклонение числа выигрышных билетов среди отобранных:

3 (билета).

в) Зададим дискретную случайную величину в виде функции распределения:

.

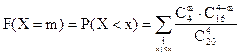Рассчитаем значения F(х):

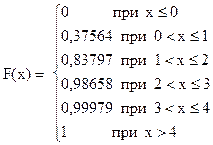
Эти данные можно представить и в виде таблицы:

Таблица 4.8.

X	x £ 0	0 < x £1	1 < x £ 2	2 < x £3	3 < x £ 4	x > 4
F(x)		0,37564	0,83797	0,98658	0,99979