Задачи к теме 4 «Законы распределения дискретных случайных величин»

1. Нефтеразведовательная компания получила финансирование для проведения 7 нефтеразработок. Вероятность успешной нефтеразведки 0,2. Предположим, что нефтеразведки осуществляют независимые друг от друга разведывательные партии.

а) Составьте ряд распределения числа успешных нефтеразведок и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что как минимум три нефтеразведки принесут успех?

2. В салоне мобильной техники представлены 4 модели телефона Samsung, 5 моделей телефона Nokia и 6 моделей телефона Motorola. В течение дня было продано 3 телефона.

а) Составьте ряд распределения числа проданных телефонов Samsung и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что в течение дня было продано как минимум два телефона Samsung?

3. Некоторый ресторан славится хорошей кухней. Управляющий ресторана утверждает, что в субботний вечер в течение получаса подходит в среднем 5 групп посетителей.

а) Составьте ряд распределения возможного числа групп посетителей ресторана в течение получаса; постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что три или более групп посетителей прибудут в ресторан в течение 60-минутного промежутка времени?

4. В кредитном отделе банка работают 5 специалистов с высшим финансовым образованием и 3 специалиста с высшим юридическим образованием. Руководство банка решило направить 3 специалистов для повышения квалификации, отбирая их в случайном порядке.

а) Составьте ряд распределения числа специалистов с высшим юридическим образованием, которые могут быть направлены на повышение квалификации и постройте его график;

б) Найдите числовые характеристики этого распределения.

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Какова вероятность того, что повышать квалификацию будут не более двух специалистов с высшим юридическим образованием?

5. Для экспертной оценки качества растворимого кофе было отобрано 9 образцов разных производителей: 6 образцов фирмы Nestle и 3 образца фирмы Kraft Food. В результате проверки выяснилось, что 4 случайно выбранных образца соответствуют стандартам качества.

а) Составьте ряд распределения числа образцов продукции фирмы Nestle, среди отобранных и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что как минимум два образца фирмы Nestle соответствуют качеству?

6. В течение часов-пик в общественном транспорте города происходит в среднем два дорожных происшествия в час. Утреннее время пик длится полтора часа, а вечернее - два часа.

а) Составьте ряды распределения числа дорожных происшествий в утренние и вечерние часы пик и постройте их графики;

б) Найдите числовые характеристики этих распределений;

в) Запишите функции распределений вероятностей и постройте их графики;

г) Чему равна вероятность того, что в определенный день в течение и утреннего, и вечернего времени не произойдет ни одного дорожного происшествия?

7. В городе 6 коммерческих банков. У каждого риск банкротства в течение года составляет 10%.

а) Составьте ряд распределения числа банков, которые могут обанкротиться в течение следующего года; постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что в течение года обанкротятся не больше двух банков?

8. В течение семестра преподаватели проводят консультации по вопросам, которые остались неясными для студентов. Преподаватель, проводящий консультации по статистике, заметил, что в среднем 12 студентов посещают его за час консультационного времени, хотя число студентов, посещающих консультацию в определенный день, в назначенный час, - случайная величина.

а) Составьте ряд распределения числа студентов, посещающих консультации преподавателя по статистике в течение получаса и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что трое студентов придут на консультацию в течение определенных 15 минут?

9.Сеть кафе «Пить кофе» включает 7 кофеен, 3 из которых имеют круглосуточный режим работы. Для оценки качества обслуживания клиентов, администрация кафе случайным образом отбирает 4 кофейни.

а) Составьте ряд распределения числа кофеен с круглосуточным режимом работы, отобранных для анализа и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что в исследовании будут участвовать не более двух круглосуточно работающих кофеен?

10. Туристическая фирма оценивает вероятность того, клиент отменит уже оплаченное путешествие вследствие личных обстоятельств как 0,15. Группа из 5 туристов оплатила тур в Индию.

а) Составьте ряд распределения числа туристов, отменивших поездку вследствие личных обстоятельств, и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите функцию распределения вероятностей и постройте ее график;

г) Определите вероятность того, что не более одного туриста отменят поездку.

11. В мастерскую по ремонту бытовой техники поступили 8 холодильников, из которых 3 подлежали гарантийному обслуживанию. Бригада специалистов, работающая в первую смену, получила наряд на ремонт 4 холодильников.

а) Составьте ряд распределения числа холодильников, отремонтированных по гарантии в первую смену; если холодильники для ремонта отбирались случайным образом, и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите функцию распределения вероятностей и постройте ее график;

г) Определите вероятность того, что по гарантии было отремонтировано не более двух холодильников.

12. Для того чтобы проверить правильность своих финансовых счетов, компания регулярно пользуется услугами аудиторов для проверки бухгалтерских проводок в счетах. Предположим, что служащие компании при обработке входящих счетов допускают примерно 5% ошибок. Пусть аудитор случайно отбирает 5 входящих документов для проверки:

а) Составьте ряд распределения числа ошибочных документов среди отобранных и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите функцию распределения вероятностей и постройте ее график;

г) Определите вероятность того, что аудитор обнаружит не менее двух ошибок.

13. В магазине имеется 11 автомобилей определенной марки. Среди них - 6 автомобилей черного цвета, 3 - серого и 2 - белого. Представители фирмы обратились в магазин с предложением о продаже им трех автомобилей этой марки, безразлично какого цвета.

а) Составьте ряд распределения числа проданных автомобилей черного цвета при условии, что автомобили отбирались случайно и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Напишите функцию распределения вероятностей и постройте ее график;

г) Какова вероятность того, что среди проданных фирме автомобилей окажется, по крайней мере, 2 автомобиля черного цвета?

14. В международном аэропорту время прибытия самолетов различных рейсов высвечивается на электронном табло. Появление информации о различных рейсах происходит случайно и независимо друг от друга. В среднем в аэропорт прибывает 6 рейсов в течение получаса.

а) Составьте ряд распределения числа сообщений о прибытии самолетов в течение получаса и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что в течение получаса появится информация о прибытии не менее трех рейсов?

д) Чему равна вероятность того, что в течение 10 минут не появится информация о прибытии ни одного самолета?

15. Телевизионный канал рекламирует новую марку автомобилей. Вероятность того, что телезритель увидит эту рекламу, оценивается в 0,4. В случайном порядке выбраны 5 телезрителей.

а) Составьте ряд распределения числа лиц, которые могут увидеть рекламу и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что по крайней мере 2 телезрителя этого канала видели рекламу новой марки автомобиля?

16. Экзаменационный билет состоит из 5 тестовых вопросов, каждый из которых имеет 4 варианта ответа и только 1 из них верный.

а) Составьте ряд распределения числа правильных ответов в билете и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что по крайней мере 3 ответа будут правильными?

17. Менеджер ювелирного магазина утверждает, что в течение дня совершается в среднем 4 покупки.

а) Составьте ряд распределения числа покупок, совершаемых в ювелиром магазине в течение дня и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что за два дня в магазине будет совершено не более 2 покупок?

18. В подгруппе английского языка занимается 9 студентов, 4 из которых окончили школы с углубленным изучением языка. Для стажировки по бухгалтерскому учету в Англии случайным образом отбираются 3 студентов.

а) Составьте ряд распределения числа студентов, среди отобранных, углубленно изучавших английский языка и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что на стажировку будет отправлено не более двух студентов, окончивших ранее спецшколы?

19. По данным страховой компании вероятность неурожая составляет 0,3. В случае неурожая, страховая фирма обязуется выплатить страховое возмещение. Договор страхования был заключен с 5 фермерскими хозяйствами.

а) Составьте ряд распределения числа возможных выплат страхового возмещения и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, страховое возмещение будет выплачено не более трем фермерским хозяйствам?

20. На предприятии 2000 единиц оборудования определенного вида Вероятность отказа единицы оборудования в течение часа составляет 0,001.

а) Составьте ряд распределения числа отказов оборудования в течение часа и постройте его график;

б) Найдите числовые характеристики этого распределения;

в) Запишите в общем виде функцию распределения вероятностей и постройте ее график;

г) Чему равна вероятность того, что в течение часа откажут как минимум 3 единицы оборудования?

Тема 5. Непрерывные случайные величины.

Пример 5.1. На рынок поступила крупная партия говядины. Предполагается, что вес туш - случайная величина, подчиняющаяся нормальному закону распределения с математическим ожиданием а = 950 кг и средним квадратическим отклонением s = 150 кг. Определите вероятность того, что вес случайно отобранной туши:

а) окажется больше 1250 кг;

б) окажется меньше 850 кг;

в) будет находиться между 800 и 1300 кг;

г) отклонится от математического ожидания меньше, чем на 50 кг;

д) отклонится от математического ожидания больше, чем на 50 кг;

е) Найдите границы, в которых отклонение веса случайно отобранной туши от своего математического ожидания не превысит утроенного среднего квадратического отклонения (проиллюстрируйте правило трех сигм);

ж) С вероятностью 0,899 определите границы, в которых будет находиться вес случайно отобранной туши. Какова при этом условии максимальная величина отклонения веса случайно отобранной туши от своего математического ожидания?

Решение. а) Вероятность того, что вес случайно отобранной туши окажется больше 1250 кг – можно понимать как вероятность того, что вес случайно отобранной туши окажется в интервале от 1250 кг до +∞.

Формула расчета вероятности попадания в заданный интервал нормально распределенной случайной величины Х имеет вид:

,

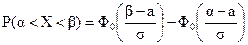где Ф₀(z) - функция Лапласа:

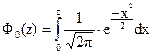
Функция Ф₀(z) является нечетной функцией; т.е. Ф₀(-z) = -Ф₀(z).

Найдем вероятность того, что вес случайно отобранной туши окажется больше 1250 кг. По условию: a = 1250, b = +¥, а = 950, s = 150.

Используем формулу расчета вероятности попадания в заданный интервал нормально распределенной случайной величины Х.

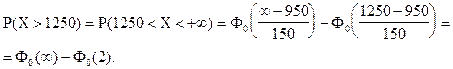
Найдем по таблице функции Лапласа (Приложение 2) значения Ф₀(z).

Значения Ф₀(+¥) в таблице нет. Однако известно, что Ф₀(z) ® 0,5 при

z ® + ¥.Уже при z = 5 Ф₀(z = 5) = 0,49999997» 0,5. Очевидно, что Ф₀(+¥) - величина бесконечно близкая к 0,5. Ф₀(-¥) - величина бесконечно близкая к -0,5.

По таблице функции Лапласа Ф₀(2) = 0,47725.

Отсюда: P(X>1250) = 0,5 - 0,47725 = 0,02275.

Итак, вероятность того, что вес случайно отобранной туши окажется больше 1250 кг, составляет 0,02275.

Проиллюстрируем решение задачи графически (рис.5.1).

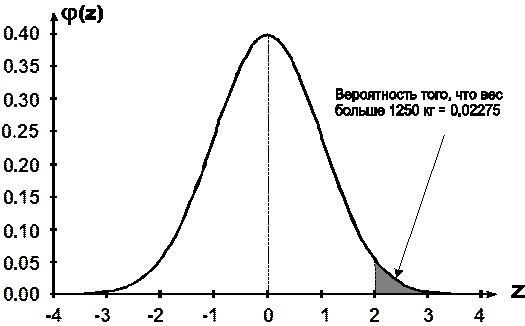
Рис.5.1 Графическая интерпретация к примеру 5.1.

Итак, нам задана нормально распределенная случайная величина Х с математическим ожиданием а = 950 кг. и средним квадратическим отклонением s = 150 кг., то есть Х ~N(950;150²). Мы хотим найти вероятность того, что Х больше 1250, то есть определить Р(Х > 1250). Преобразуем Х в Z, и тогда искомая вероятность определится по таблице Приложения 2 стандартного нормального распределения. .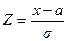

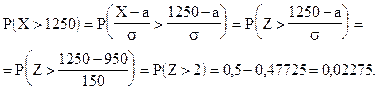
Точка z = 0 соответствует математическому ожиданию, то есть а = 950 кг.

б) Вероятность того, что вес случайно отобранной туши окажется меньше 850 кг - это, то же самое, что вероятность того, что вес случайно отобранной туши окажется в интервале от -¥ до 850 кг.

По условию: a = -¥, b = 850, а = 950, s = 150.

Для расчета искомой вероятности используем формулу расчета вероятности попадания в заданный интервал нормально распределенной случайной величины Х.

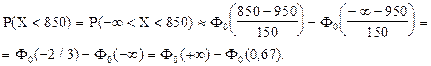
Согласно свойству функции Лапласа:

-Ф₀(-¥) = Ф₀(+¥),

а Ф₀(-0,67) = -Ф₀(0,67).

Найдем по таблице функции Лапласа (Приложение 2) значения Ф₀(z).

Ф₀(+¥)» 0,5;

Ф₀(0,67) = 0,24857.

Отсюда: P(X < 850) = 0,5 - 0,24857 = 0,25143.

Вероятность того, что вес случайно отобранной туши окажется меньше 850 кг составляет 0,25143.

Проиллюстрируем решение задачи графически (рис. 5.2).

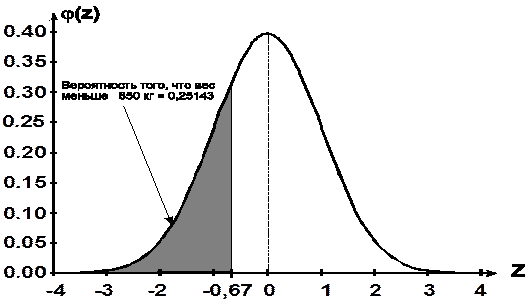
Рис.5.2. Графическая интерпретация к примеру 5.1.

По условию данной задачи точка на оси абсцисс (z = -0,67) соответствует х = 850, т.е. весу, равному 850 кг. Заштрихованная на графике площадь представляет собой вероятность того, что вес наудачу выбранной туши окажется меньше 850 кг, т.е. в интервале от -¥ до 850 кг.

в) Найдем вероятность того, что вес случайно отобранной туши окажется в интервале от 800 до 1300 кг.

По условию: a = 800, b = 1300, а = 950, s = 150.

Для расчета искомой вероятности используем формулу расчета вероятности попадания в заданный интервал нормально распределенной случайной величины Х.

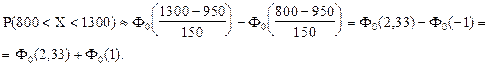
Согласно свойству функции Лапласа:

-Ф₀(-1) = Ф₀(1).

Найдем по таблице функции Лапласа (Приложение 2) значения Ф₀(z).

Ф₀(2,33) = 0,49010;

Ф₀(1) = 0,34134.

Отсюда: P(800 < X< 1300) = 0,49010 + 0,34134 = 0,83144.

Вероятность того, что вес случайно отобранной туши окажется в интервале от 800 кг до 1300 составляет 0,83144.

Проиллюстрируем решение задачи графически (рис. 5.3).

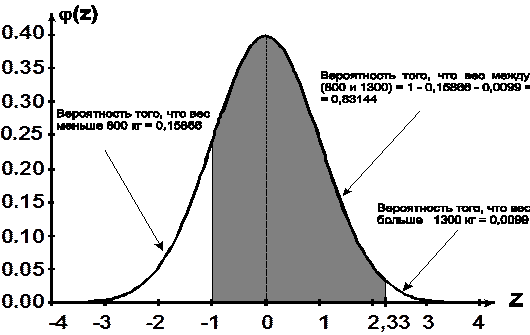
Рис.5.3. Графическая интерпретация к примеру 5.1.

По условию данной задачи точка на оси абсцисс (z = -1) соответствует х = 800, т.е. весу, равному 800 кг, а точка (z = 2,33) соответствует х = 1300, т.е. весу, равному 1300 кг. Заштрихованная на графике площадь представляет собой вероятность того, что вес наудачу выбранной туши окажется в интервале от 800 до 1300 кг.

На графике видно, что искомую вероятность, что вес наудачу выбранной туши окажется в интервале от 800 до 1300 кг, можно было найти другим способом. Для этого необходимо было найти вероятность того, вес наудачу выбранной туши окажется меньше 800 кг, а также- больше 1300 кг, Полученные вероятности – сложить и вычесть из единицы.

Так, вероятность того, вес наудачу выбранной туши окажется меньше 800 кг - это, другими словами, вероятность того, что вес случайно отобранной туши окажется в интервале от -¥ до 850 кг.

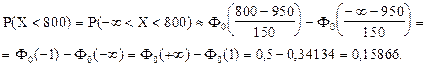
Вероятность того, что вес случайно отобранной туши окажется больше 1300 кг - это, другими словами, вероятность того, что вес случайно отобранной туши окажется в интервале от 1300 кг до +¥.

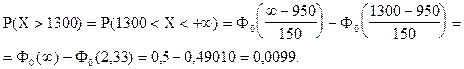
Отсюда, искомая вероятность того, что вес наудачу выбранной туши окажется в интервале от 800 до 1300 кг:

Р(800 < Х < 1300) = 1 - (P(X<800) + P(X>1300)) = 1 - (0,15866 + 0,0099) =

=1 - 0,16856 = 0,83144.

г) Найдем вероятность того, что вес случайно отобранной туши отклонится от математического ожидания меньше, чем на 50 кг, т.е.:

P(½X - 950½< 50) =?

Что значит: ½X - 950½< 50?

Это неравенство можно заменить двойным неравенством:

-50 < X - 950 < 50 или

950 - 50 < X < 950 + 50,

900 < X < 1000.

Следовательно:

P½X - 950½< 50) = Р(900 < Х < 1000).

А это вероятность попадания в заданный интервал нормально распределенной случайной величины Х.

Отсюда:

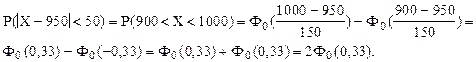
Согласно свойству функции Лапласа:

-Ф₀(-0,33) = Ф₀(0,33).

Найдем по таблице функции Лапласа (Приложение 2) значения Ф₀(z).

Ф₀(0,33) = 0,1293.

Следовательно:

P(½X - 950½< 50) = Р(900 < Х < 1000) = 2 × 0,1293 = 0,2586.

Вероятность того, что вес случайно отобранной туши отклонится от математического ожидания меньше, чем на 50 кг, составляет 0,2586.

Эту задачу легче решить, используя формулу расчета вероятности заданного отклонения нормально распределенной случайной величины Х от своего математического ожидания:

где - D величина отклонения случайной величины Х от математического ожидания.

По условию D = 50; а = 950, s = 150.

Используя эту формулу, сразу получим:

P(½X - 950½< 50) = 2Ф₀(50 / 150) = 2Ф₀(0,33) = 2 × 0,1293 = 0,2586.

Проиллюстрируем решение задачи графически (рис. 5.4).

Рис.5.4. Графическая иллюстрация к задаче 5.1.

По условию данной задачи точка на оси абсцисс (z = -0,33) соответствует х = 900, т.е. весу, равному 900 кг, а точка (z = 0,33) соответствует х = 1000, т.е. весу, равному 1000 кг. Заштрихованная на графике площадь представляет собой вероятность того, что вес наудачу выбранной туши окажется в интервале от 900 до 1000 кг., т.е. отклонится от математического ожидания меньше, чем на 50 кг.

д) Найдем вероятность того, что вес случайно отобранной туши отклонится от математического ожидания больше, чем на 50 кг, т.е.:

P(½X - 950½> 50) =?

Это вероятность события, противоположного по отношению к событию: вес случайно отобранной туши отклонится от математического ожидания меньше, чем на 50 кг (P(½X - 950½< 50)).

Следовательно:

P(½X - 950½> 50) = 1 - P(½X - 950½< 50) = 1 - 0,2586 = 0,7414.

Вероятность того, что вес случайно отобранной туши отклонится от математического ожидания больше, чем на 50 кг, составляет 0,7414.

Можно использовать другой алгоритм решения.

Вероятность того, что вес случайно отобранной туши отклонится от математического ожидания больше, чем на 50 кг, - это вероятность того, что вес случайно отобранной туши будет или меньше (950 - 50 = 900) кг или больше (950 + 50 = 1000) кг.

По теореме сложения вероятностей несовместных событий имеем:

P(½X - 950½> 50) = P(X < 900) + P(X > 1000).

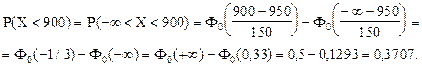
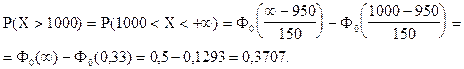
Отсюда:

P(½X - 950½> 50) = P(X < 900) + P(X > 1000) = 0,3707 + 0,3707 = 0,7414.

е) Найдем границы, в которых отклонение веса случайно отобранной туши от своего математического ожидания не превысит утроенного среднего квадратического отклонения.

В этом задании студентам предлагается проиллюстрировать правило трех сигм, которое можно сформулировать следующим образом:

Если случайная величина распределена по нормальному закону, то ее отклонение от математического ожидания практически не превышает ±3s.

Р(½Х - а ½<3s) = 2Ф₀(3) = 0,9973.

Вероятность того, что отклонение нормально распределенной случайной величины Х от своего математического ожидания будет меньше 3s или, другими словами, вероятность того, что нормально распределенная случайная величина Х попадет в интервал (а - 3s; а + 3s), равна 0,9973.

Следовательно, вероятность того, что отклонение случайной величины от своего математического ожидания по абсолютной величине превысит утроенное среднее квадратическое отклонение, очень мала и равна 0,0027. Другими словами, лишь в 27 случаях из 10000 случайная величина Х в результате испытания может оказаться вне интервала (а - 3s; а + 3s). Такие события считаются практически невозможными.

Формулу, описывающую правило трех сигм, несложно получить из формулы вероятности заданного отклонения нормально распределенной случайной величины Х от своего математического ожидания:

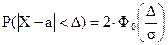
Если взять D = 3s, то получим D /s = 3.

Отсюда:

Р(½Х - а ½< 3s) = 2Ф₀(3) = 0,9973.

По условию задачи: а = 950; s = 150.

Правило трех сигм можно представить так:

Р(а - 3s < Х < a + 3s) = 2Ф₀(3) = 0,9973.

Интересующие нас границы - это границы интервала (а - 3s; a + 3s), т.е.:

а - 3s< Х < a + 3s,

950 – 3 × 150 < X < 950 + 3 × 150,

500 < X < 1400.

Учитывая, что вес отобранной туши - нормально распределенная случайная величина, можно быть практически уверенным, что вес случайно отобранной туши не выйдет за пределы от 500 до 1400 кг.

ж) Определим границы, в которых с вероятностью 0,899 будет находиться вес случайно отобранной туши.

Формулу вероятности заданного отклонения нормально распределенной случайной величины Х от своего математического ожидания можно представить следующим образом:

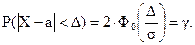
или

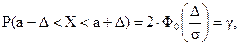
где g - вероятность того, что отклонение нормально распределенной случайной величины Х от своего математического ожидания не превысит заданной величины D.

По условию задачи: а = 950; s = 150.

Используя последнюю формулу, получим:

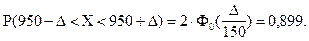
Из соотношения: 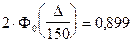, найдем D.

,

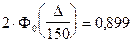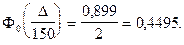
По таблице функции Лапласа (Приложение 2) найдем, при каком z =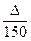

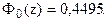
z = 1,64, т.е.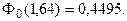

Отсюда: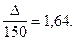

D= 1,64 × 150 = 246.

С вероятностью 0,899 можно ожидать, что отклонение веса случайно отобранной туши от своего математического ожидания не превысит 246 кг.

Найдем границы интересующего нас интервала:

а - D < Х < a + D,

950 - 246 < X < 950 + 246,

704 < X < 1196.

С вероятностью 0,899 можно ожидать, что вес случайно отобранной туши будет находиться в пределах от 704 до 1196 кг.

Ответ:а) 0,02275; б) 0,25143; в) 0,83144; г) 0,2586; д) 0,7414;

е) (500; 1400); ж) 246; (704; 1196).

Пример 5.2. Изменим условие предыдущей задачи.

На рынок поступила крупная партия говядины. Предполагается, что вес туш – случайная величина, подчиняющаяся нормальному закону распределения с неизвестным математическим ожиданием и средним квадратическим отклонением s =150 кг. Известно, что 37,07% туш имеют вес более 1000 кг. Определите ожидаемый вес случайно отобранной туши.

Решение. По условию задачи: s = 150; a = 1000; b = +¥; P(X > 1000) = 0,3707.

Ожидаемый вес случайно отобранной туши - это среднеожидаемый вес, математическое ожидание, т.е. а =?

Используем формулу (5.10) расчета вероятности попадания в заданный интервал нормально распределенной случайной величины Х:

;

;

;

.

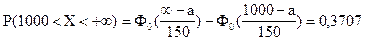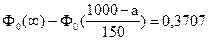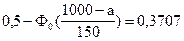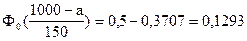По таблице функции Лапласа (Приложение 2) найдем, при каком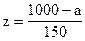

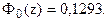
z = 0,33, т.е.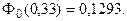

Отсюда: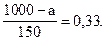

1000 - а = 0,33 × 150 = 50.

а = 1000 - 50 = 950.

Ответ. Среднеожидаемый вес случайно отобранной туши составляет 950 кг.

Пример 5.3. Вновь изменим условие задачи.

На рынок поступила крупная партия говядины. Предполагается, что вес туш - случайная величина, подчиняющаяся нормальному закону распределения с математическим ожиданием а = 950 кг и неизвестным средним квадратическим отклонением. Известно, что 15,87% туш имеют вес менее 800 кг. Определите среднее квадратическое (стандартное) отклонение веса туш.

Решение. По условию задачи: а = 950; a = -¥ b = 800; P(X < 800) = 0,1587; s =?

Используем формулу (5.10) расчета вероятности попадания в заданный интервал нормально распределенной случайной величины Х:

;

;

;

;

.

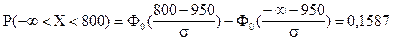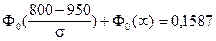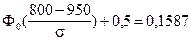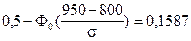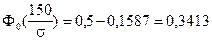По таблице функции Лапласа (Приложение 2) найдем, при каком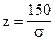

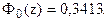
z = 1, т.е.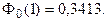

Отсюда: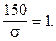

s= 150.

Ответ. Среднее квадратическое отклонение веса туш составляет 150 кг.

Пример 5.4. Еще раз изменим условие задачи.

На рынок поступила крупная партия говядины. Предполагается, что вес туш - случайная величина, подчиняющаяся нормальному закону распределения с неизвестными математическим ожиданием и средним квадратическим отклонением. Известно, что 15,87% туш имеют вес менее 800 кг и 37,07% туш имеют вес более 1000 кг. Определите среднеожидаемый вес и среднее квадратическое (стандартное) отклонение веса туш.

Решение. По условию задачи: a = -¥; b = 800; P(X < 800) = 0,1587;

P(X > 1000) = 0,3707; a =?; s =?

Используем формулу (5.10) расчета вероятности попадания в заданный интервал нормально распределенной случайной величины Х:

;

;

;

;

.

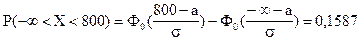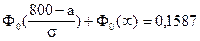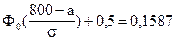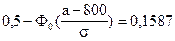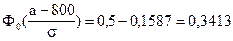По таблице функции Лапласа (Приложение 2) найдем, при каком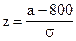

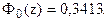
z = 1, т.е.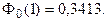

Отсюда: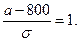

С другой стороны:

;

;

;

.

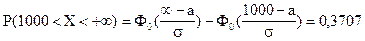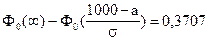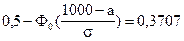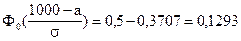По таблице функции Лапласа (Приложение 2) найдем, при каком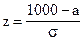

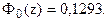
z = 0,33, т.е.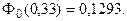

Отсюда: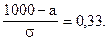

Решим систему линейных уравнений:

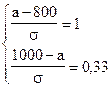
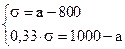
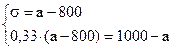
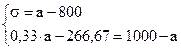
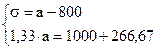
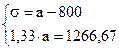
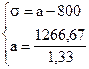
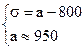
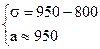
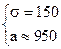
Среднеожидаемый вес случайно отобранной туши составляет 950 кг. Среднее квадратическое отклонение веса туш - 150 кг.

Ответ: а = 950; s = 150.

Пример 5.5. В очередной раз изменим условие задачи.

На рынок поступила крупная партия говядины. Предполагается, что вес туш - случайная величина, подчиняющаяся нормальному закону распределения с математическим ожиданием а = 950 кг и неизвестным средним квадратическим отклонением. Каким должно быть среднее квадратическое (стандартное) отклонение, чтобы с вероятностью 0,81648 можно было утверждать, что абсолютное отклонение веса случайно отобранной туши от математического ожидания не превысит 200 кг?

Решение. По условию задачи: а = 950; D = 200; P(½X - 950½< 200) = 0,81648; s =?

Используем формулу (5.11) расчета вероятности попадания заданного отклонения нормально распределенной случайной величины Х от своего математического ожидания:

Тогда получим:

P(½X - 950½< 200) = 2Ф₀(200 / s) = 0,81648;

2Ф₀(200 / s = 0,81648;

Ф₀(200 / s) = 0,81648 / 2;

Ф₀(200 / s) = 0,40824.

По таблице функции Лапласа (Приложение 2) найдем, при каком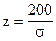

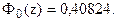
z = 1,33, т.е.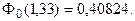

Отсюда: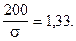

s = 200 / 1,33 = 150.

Ответ. Чтобы с вероятностью 0,81648 можно было утверждать, что абсолютное отклонение веса случайно отобранной туши от математического ожидания не превысит 200 кг, среднее квадратическое отклонение веса туш должно составлять 150 кг.

Пример 5.6 Фирма собирается приобрести партию из 100 000 единиц некоторого товара. Из прошлого опыта известно, что 1% товаров данного типа имеют дефекты. Какова вероятность того, что в данной партии окажется от 950 до 1050 дефектных единиц товара?

Решение. В качестве случайной величины в данной задаче выступает число дефектных единиц товара в общей партии из 100000 единиц. Обозначим ее через X.

Перечислим все возможные значения случайной величины Х: 0, 1, 2,..., 99999, 100000.

Это - дискретная случайная величина, т.к. ее возможные значения отличаются друг от друга не менее чем на 1, и множество ее возможных значений является счетным.

По условию вероятность того, что единица товара окажется дефектной, - постоянна и составляет 0,01 (p = 0,01). Вероятность противоположного события, т.е. того, что единица товара не имеет дефекта - также постоянна и составляет 0,99 (q = 1—p = 1—0,01 = 0,99).

Все 100000 испытаний - независимы, т.е. вероятность того, что каждая единица товара окажется дефектной, не зависит от того, окажется дефектной или нет любая другая единица товара.

Значения случайной величины Х - это, в общем виде, число появлений интересующего нас события в 100000 независимых испытаниях.

Это позволяет сделать вывод о том, что случайная величина Х - число дефектных единиц товара в общей партии из 100000 единиц - подчиняется биномиальному закону распределения вероятностей с параметрами n = 100000 и p = 0,01.

Итак, по условию задачи: n = 100000; p = 0,01; q = 0,99, X = m.

Необходимо найти вероятность того, что число дефектных единиц товара окажется в пределах от m₁ = 950 до m₂ =1050, т.е. - вероятность того, что случайная величина X = m попадет в интервал от 950 до 1050, т.е.:

P(m₁ < m < m₂) =?

Так как мы имеем дело со случайной величиной, подчиняющейся биномиальному распределению, вероятность появления события m раз в n независимых испытаниях необходимо вычислять по формуле Бернулли (4.9).

В данном случае, для определения искомой вероятности нам необходимо с помощью формулы Бернулли найти P_{100000, 950}; P_{100000, 951}; P_{100000, 952};...; P_{100000, 1049}; P_{100000, 1050}, а затем - сложить их, используя теорему сложения вероятностей несовместных событий.

Очевидно, что такой способ определения искомой вероятности связан с громоздкими вычислениями. Так, например:

.

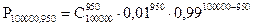Можно значительно облегчить расчеты, если аппроксимировать биномиальное распределение нормальным, т.е. выразить функции биномиального распределения через функции нормального.

Когда n - число испытаний в биномиальном эксперименте - возрастает, дискретное биномиальное распределение стремится к непрерывному нормальному распределению. Это означает, что для больших n мы можем аппроксимировать биномиальные вероятности вероятностями, полученными для нормально распределенной случайной величины, имеющей такое же математическое ожидание и такое же среднее квадратическое отклонение.

Подставим параметры биномиального распределения (5.15) в формулу (5.10) и получим формулу для приближенного расчета вероятности появления события от m₁ и до m₂ раз в n независимых испытаниях P(m₁ < m > m₂):

,

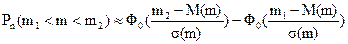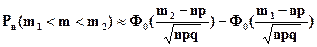, (5.19)

где Ф ₀(z) - функция Лапласа: .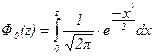

Формулу для приближенного вероятности появления события не менее m₁ и не более m₂ раз в n независимых испытаниях P_n(m₁ < m < m₂) называют интегральной теоремой Лапласа.

Использование локальной и интегральной теорем Лапласа дает приближенные значения искомых вероятностей. Погрешность будет невелика при условии, что

npq > 9.

Для решения данной задачи воспользуемся интегральной теоремой Лапласа:

;

;

;

;

.

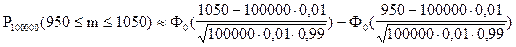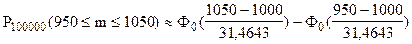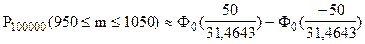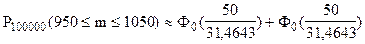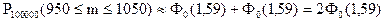По таблице функции Лапласа (Приложение 2) найдем Ф₀(1,59):

Ф₀(1,59) = 0,44408.

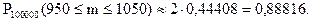
Вероятность того, что в партии из 100000 единиц окажется от 950 до 1050 дефектных единиц товара, составляет 0,88816.

Данную конкретную задачу можно было решить еще более просто.

Математическое ожидание числа дефектных единиц товара равно 1000 единиц:

M(m) = n × p = 100000 × 0,01 = 1000.

Абсолютное отклонение нижней и верхней границ интервала [m₁; m₂] от математического ожидания M(m) = n × p составляет 50 единиц:

½m₁ – n × p½=½950 – 100000 × 0,01½= 50;

½m₂ - n × p½=½1050 – 100000 × 0,01½= 50.

Следовательно, искомую вероятность можно рассматривать как вероятность заданного отклонения частоты от своего математического ожидания:

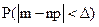
Подставив параметры биномиального распределения в формулу расчета вероятности заданного отклонения нормально распределенной случайной величины от своего математического ожидания, получим формулу для приближенного расчета вероятности заданного отклонения частоты от своего математического ожидания:

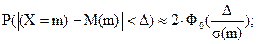
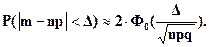(5.20)

При использовании этой формулы для решения задачи сразу получим:

;

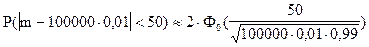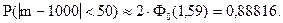
Ответ. Вероятность того, что в партии из 100000 единиц окажется от 950 до 1050 дефектных единиц товара, составляет 0,88816.

Пример 5.7. Подлежат исследованию 400 проб руды. Вероятность промышленного содержания металла в каждой пробе для всех проб одинакова и равна 0,8. Найти вероятность того, что доля проб с промышленным содержанием металла отклонится от вероятности промышленного содержания металла в каждой пробе не более чем на 0,05.

Решение. В отличие от предыдущей задачи, в данном случае речь идет о расчете вероятности заданного отклонения частости (относительной частоты) появления события от вероятности его появления в отдельном независимом испытании, т.е.:

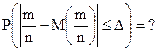
По условию: n = 400; p = 0,8; q = 1- 0,8 = 0,2; D = 0,05.

;

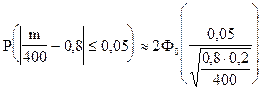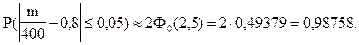
Ответ. Вероятность того, что доля проб с промышленным содержанием металла отклонится от вероятности промышленного содержания металла в каждой пробе не более чем на 0,05, составляет 0,98758.