Подставим выражение 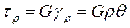 в формулу
в формулу 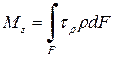 :
:
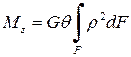
С учетом того, что интеграл в полученной формуле представляет собой полярный момент инерции поперечного сечения, получим иную форму закона Гука при кручении вала: 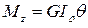 , где для круглого стержня формула полярного момента через диаметр:
, где для круглого стержня формула полярного момента через диаметр: 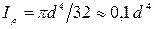 .
.
Формула относительного угла закручивания: 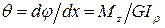
Из формулы относительного угла закручивания следует, что произведение модуля сдвига и полярного момента 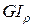 характеризует жесткость стержня при кручении. Напомним, что модуль сдвига (
характеризует жесткость стержня при кручении. Напомним, что модуль сдвига (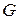 ) характеризует жесткость материала при сдвиге (кручении).
) характеризует жесткость материала при сдвиге (кручении).
Условие жесткости при кручении
За меру жесткости при кручении принимается относительный угол закручивания вала (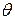 ). Формула условия жесткости при кручении:
). Формула условия жесткости при кручении:
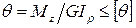 , где
, где 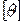 – значение допускаемого относительного угла закручивания, град/м, зависящее от назначения вала.
– значение допускаемого относительного угла закручивания, град/м, зависящее от назначения вала.
10. Поперечный изгиб. Поперечная сила и изгибающий момент.
Поперечный изгиб – изгиб, при котором в сечениях стержня кроме внутреннего изгибающего момента возникает и поперечная сила. Строго говоря, к простым видам сопротивления относится лишь чистый изгиб; поперечный изгиб относят к простым видам сопротивления условно, так как в большинстве случаев (для достаточно длинных балок) действием поперечной силы при расчетах на прочность можно пренебречь. При определении внутренних усилий будем придерживаться следующего правила знаков:
|
|
|
1) поперечная сила Qy считается положительной, если она стремится повернуть рассматриваемый элемент балки по часовой стрелке;
2) изгибающий момент Мz считается положительным, если при изгибе элемента балки верхние волокна элемента оказываются сжатыми, а нижние – растянутыми (правило зонта).
В сечениях балки возникают два внутренних силовых фактора: изгибающий момент Мх и поперечная сила Qy
1. В сечении, где приложена сосредоточенная сила, - на эпюре Qy скачок по модулю равный этой силе, на эпюре Мх – излом навстречу силе.
2. В сечении, где приложена сосредоточенная пара сил, - на эпюре Мх скачок по модулю равный этой паре сил. На эпюре Qy это не сказывается.
3.Если на участке имеется равномерно распределенная нагрузка, то Qy изменяется по линейному закону, Мх – по параболе, выпуклостью навстречу нагрузке q (Мх = Мэкстр – в сечении, где Qy меняет свой знак)
Изгибающий момент — момент внешних сил относительно сечения балки.
Для балки, изображенной на рисунке,
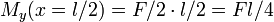
 2015-01-30
2015-01-30 3436
3436








