Веществу можно приписывать довольно большое количество характеристик: массу, заряд, объем и т. д. Для информации имеется не столь большой, но достаточно представительный набор характеристик. У отдельных характеристик информации имеются единицы измерения, что позволяет некоторой ее порции приписывать числа - количественные характеристики информации.
С практической точки зрения информация всегда представляется в виде сообщения. Однако между количеством информации и длиной сообщения нет однозначной зависимости. Как вес груза не определяет его ценность, так и длительность сообщения не определяет то количество информации, которое содержит в себе это сообщение. Каким же образом определяется количество информации в сообщении?
На сегодняшний день наиболее известны три способа измерения информации: объемный, энтропийный и алгоритмический.
Объемный – это самый простой и грубый способ измерения информации (поэтому количественную оценку информации называют - объемом информации).
Объем информации в сообщении - это количество символов в сообщении.
Поскольку сообщение, например, одно и то же число может быть записано разными способами (с использованием разных алфавитов):
"двадцать пять"
XXV,
то этот способ чувствителен к форме представления (записи) сообщения.
. Энтропийный подход к информации - как к мере уменьшения неопределенности знания позволяет количественно измерять информацию. Получатель информации (сообщения) имеет определенные представления о возможных наступлениях некоторых событий. Эти представления в общем случае недостоверны и выражаются вероятностями, с которыми он ожидает то или иное событие Общая мера неопределенности (энтропия) характеризуется некоторой зависимостью от этих вероятностей Количество информации в сообщении определяется тем, насколько уменьшится эта мера после получения сообщения.
Пусть у нас имеется монета, которую мы бросаем на ровную поверхность. С равной вероятностью произойдет одно из двух возможных событий – выпадет "орел" или "решка". Можно говорить, что события равновероятны, если при возрастающем числе опытов число выпадений "орла" и "решки" постепенно сближаются.
Перед броском существует неопределенность нашего знания (возможны два события), и как упадет монета - предсказать невозможно. После броска наступает полная определенность, так как мы видим (получаем зрительное сообщение), что монета в данный момент находится в определенном положении (например, "орел"). Это сообщение приводит к уменьшению неопределенности нашего знания в два раза, т.к. из двух возможных равновероятных событий реализовалось одно.
В окружающей действительности чаще встречаются ситуации, когда может произойти большее, чем два, число равновероятных событий. Так, при бросании шестигранного игрального кубика – существует 6 равновероятных событий.
Чем больше начальное число возможных равновероятных событий, тем больше начальная неопределенность нашего знания и, соответственно, тем большее количество информации будет содержать сообщение о результатах опыта.
За меру количества информации (I) в сообщении принимается величина изменения неопределенности êН (энтропии), вызванная этим сообщением.
I = êН = Н н – Н к
Если после получения сообщения конечная неопределенность Н кобратится в нуль, то первоначальное неполное знание заменится полным знанием и количество информации станет равной начальной неопределенности I = Н н. Иными словами начальная неопределенность Н н – это мера недостающей информации.
Существует множество ситуаций, когда возможные события имеют различные вероятности исхода. Например, если у монеты одна сторона тяжелее другой, то при ее бросании вероятности выпадения "орла" и "решки" будут различаться.
Неопределенность события Н н., имеющего N возможных исходов с различными вероятностями, согласно формуле Шеннона, р а вна:
Н н = - 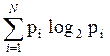
 2014-10-30
2014-10-30 1149
1149
