2015-01-30
549
Рассмотрим задачу синтеза адаптивного управления для случай каскадного соединения нелинейных подсистем, когда выход одной подсистемы можно рассматривать в качестве управляющего воздействия для другой подсистемы. К данному виду относятся многие технические и технологические системы управления и в ряде случаев могут быть к ним приведены с помощью эквивалентных преобразований.
Пусть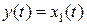 
является регулируемой координатой для ОУ представленного каскадной системой дифференциальных уравнений:
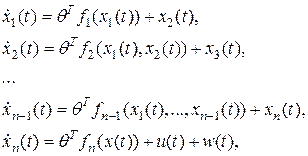(2.7)
где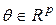 
– вектор неизвестных априори параметров системы, 
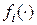– гладкие функции своих аргументов.
Ставится задача построения закона управления
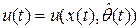, (2.8)
при котором в замкнутой системе при произвольных ограниченных внешних воздействиях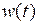 
обеспечивается заданная точность:
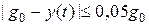при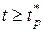 
. (2.9)
Известны различные подходы к решению данной задачи. Наиболее распространенной стратегией отыскания закона управления (2.8) является двухэтапный синтез. На первом этапе ставится задача отыскания обратной связи вида
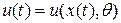, (2.10)
обеспечивающей достижение целей управления при условии, что значения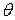 
известны. На втором этапе вектор 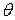в выражении (2.10) формально заменяют оценкой 
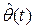, которая строится с помощью уравнения
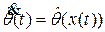, (2.11)
и находят уравнение (2.11), гарантирующее достижение цели управления с учетом ограничений задачи (неполноту информации, ограничение на управление и др.).
В этом случае задача синтеза адаптивного регулятора при соблюдении условий устойчивости системы разбивается на две независимые задачи. Это позволяет использовать известные методы синтеза управления (2.10) для нелинейных систем, и с другой стороны применять различные алгоритмы построения оценки (2.11).
В такой постановке задачи не рассматриваются возможности повышения качества процессов управления за счет учета динамики процесса адаптации (2.11) и построения соответствующего закона управления (2.8). Учет процесса адаптации при выборе закона управления относится к задачам прямого адаптивного управления, рассмотренных в работе [3]. Однако в [3] не учитывается влияние возмущений, которые существенно влияют на процесс адаптации. Ниже рассматривается подход к синтезу управления (2.8), совмещенного с процессом адаптации (2.11), при наличии возмущений с использованием принципа локализации [20], рассмотренного ранее в работе [14].
С целью выполнения условия (2.9) для регулируемой координаты 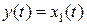используем эталонную модель 
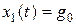и введем отклонение 
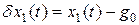, которое подчиним уравнению
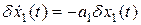, (2.12)
где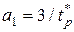 
. Тогда из первого уравнения системы (2.7) с учетом 
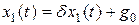получим выражение
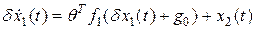. (2.13)
Координату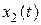 
с учетом (2.12) представим в виде:
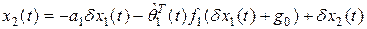, (2.14)
где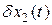 
– неизвестная переменная, 
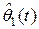– вектор настраиваемых параметров, удовлетворяющий уравнению
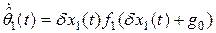. (2.15)
Тогда придем к системе уравнений
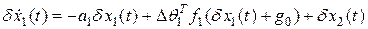, (2.16)
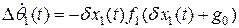, (2.17)
где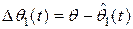 
, переменная 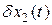выбирается из условия устойчивости
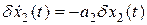, (2.18)
где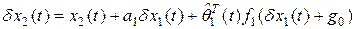 
.
Если в дальнейшем удастся выполнить условие (2.18), то в уравнении (2.16) переменная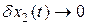 
при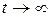 
. Тогда выполняется условие 
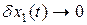при 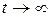, поскольку производная по времени функции Ляпунова
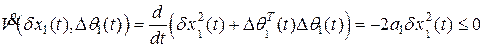. (2.19)
Однако, относительно вектора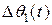 
можно утверждать только, что 
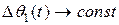при .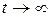
Выполняя последовательно указанные выше операции, получим выражение для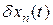 
, от которого возьмем производную по времени. В результате получим выражение, в которое входят управление 
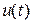, известные 
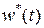и неизвестные 
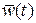функции. При этом полагаем 
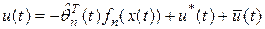, где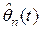 
– является решением уравнения
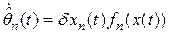, (2.20)
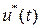– компенсирует 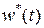, а управление 
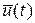– компенсирует 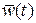с помощью принципа локализации:
.
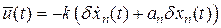Особенностью управления 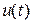по сравнению с ранее рассмотренным способом синтеза в работе [14] является возможность оценивать вектор неизвестных параметров системы и проводить компенсацию известных функций, что позволяет снизить коэффициент усиления в выражении (2.20).
Для сравнения данного способа синтеза адаптивного управления рассмотрим тестовую задачу из работы [3].
Пример 2.1. Пусть задана система второго порядка
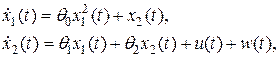(2.21)
где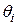 
, 
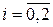– неизвестные априори постоянные параметры, 
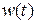– ограниченное неизвестное возмущение, задается значение 
.
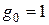Уравнения (2.16), (2.17) будут иметь вид
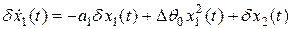, (2.22)
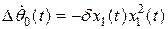, (2.23)
где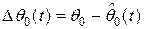 
, оценка 
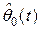является решением уравнения
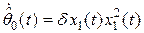. (2.24)
Производная переменной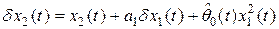 
с учетом (2.24) имеет вид
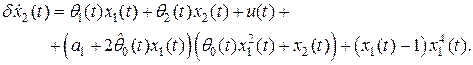(2.25)
Оценка параметров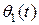 
, 
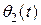осуществляется с помощью алгоритма
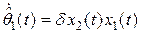, (2.26)
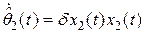. (2.27)
Уравнение (2.25) перепишем в виде
,
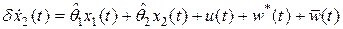где 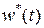и 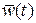– известное и неизвестное приведенные возмущения:
,
.
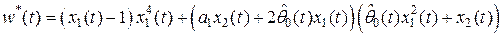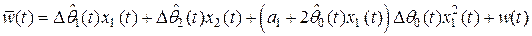Тогда получим адаптивный закон управления
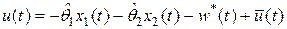, (2.28)
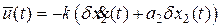. (2.29)
Для вычисления 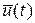можно воспользоваться приближенным выражением
.
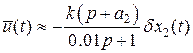Проведем моделирование замкнутой системы (2.21), (2.26)-(2.29) при исходных данных принятых в работе [3]: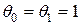 
, 
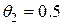; возмущение отсутствует, т.е. 
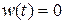; начальные условия 
, 
.
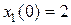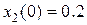На рисунках 2.1-.2.4 приведены переходные процессы координат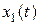 
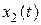, , управления 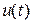и оценки точности идентификации параметров 
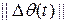, равной
.
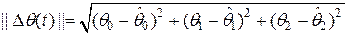В работе [3] проведено сравнение различных алгоритмов управления и наилучшим признан алгоритм авторов, при котором время регулирования составляет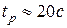 
, спустя время 
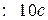значение 
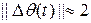, значение критерия качества, характеризующего затраты энергии на управление 
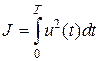, при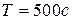 
равно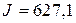 
.
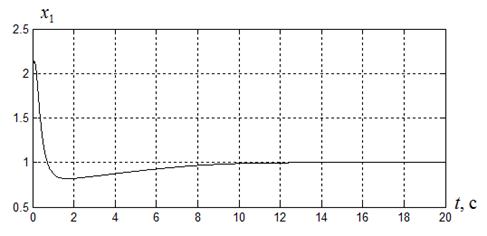
Рисунок 2.1
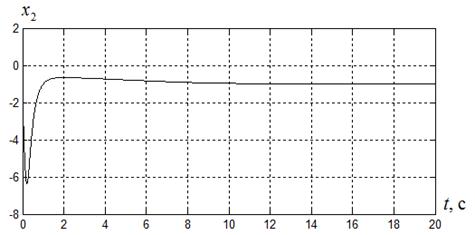
Рисунок 2.2
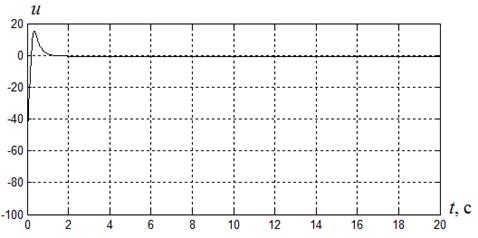
Рисунок 2.3
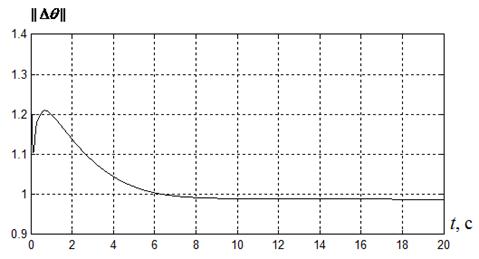
Рисунок 2.4
Как следует из рисунков 2.1-2.2 здесь при заданных параметрах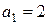 
, введении ограничения на управление 
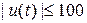, получено время регулирования 
, 
, 
.
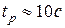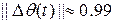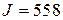Также проводилось моделирование динамики системы при наличии возмущающего воздействия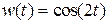 
. При этом переходные процессы рисунков 2.1-2.4 практически не изменились.
Таким образом, предложенный закон управления (2.26)-(2.29) существенно превосходит указанные в работе [3] алгоритмы адаптивного управления объектом (2.21).
Продолжим рассмотрение данного примера, используя другой подход к синтезу управления на основе идентификации неопределенных возмущений в системе.
Исходную систему (2.21) перепишем в виде
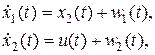(2.30)
где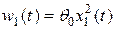 
, 
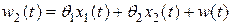– неизвестные воздействия.
Для решения задачи будем оценивать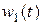 
для использования в законе управления, а воздействие 
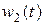подавлять с помощью управляющего сигнала .
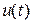Используем предложенный в работе [14] способ оценивания нерегулярных внешних воздействий. Здесь нетрудно показать, что наблюдающее устройство имеет вид
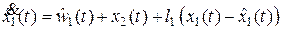, (2.31)
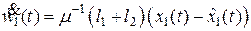, (2.32)
где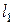 
, 
, 
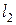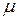– выбираемые параметры.
Введем отклонение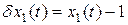 
, которое подчиним уравнению
,
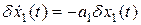из которого найдем выражение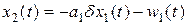 
. Найдем производную по времени для отклонения 
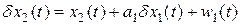, которую представим в виде:
,
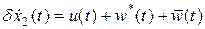где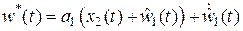 
, 
.
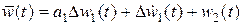Тогда закон управления будет иметь вид
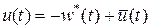, (2.33)
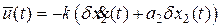. (2.34)
Проведем моделирование замкнутой системы (2.30)-(2.34) при тех же исходных данных, для принятых параметров: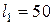 
, 
, 
.
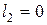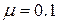На рисунках 2.5-.2.8 приведены переходные процессы координат 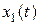, , 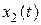управления , , 
.
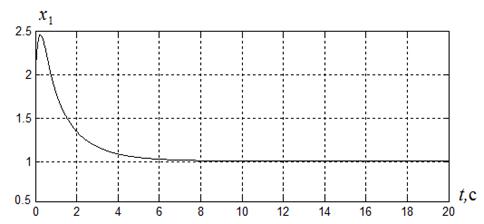
Рисунок 2.5
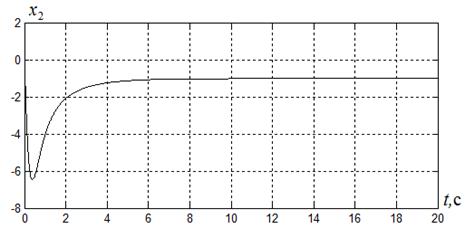
Рисунок 2.6
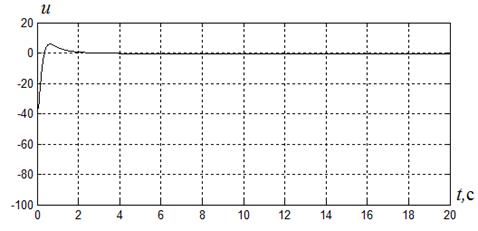
Рисунок 2.7
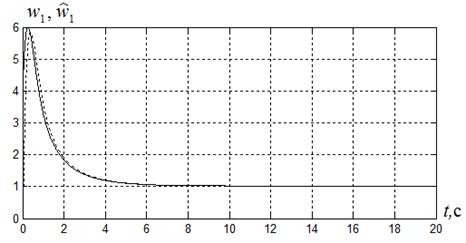
Рисунок 2.8
Как следует из рисунков 2.5-2.7 здесь при заданных параметрах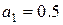 
, 
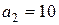и отсутствии в законе управления (2.33) компенсирующей составляющей 
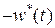, управление ограничено, т.е. 
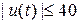. При этом время регулирования 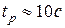, а значение критерия 
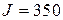. При учете в управлении (2.33) компенсирующей составляющей 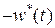переходные процессы не изменяются, кроме управляющего сигнала 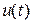, который ограничен неравенством 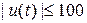, при этом значение критерия 
.
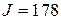На рисунке 2.8 приведены для сравнения график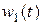и и 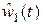(пунктирная линия), иллюстрирующие работоспособность алгоритма оценивания возмущения.
Также проводилось моделирование динамики системы при наличии возмущающего воздействия 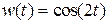. При этом переходные процессы рисунков 2.5-2.7 практически не изменились.
Таким образом, предложенный закон управления (2.31)-(2.34) проще закона управления (2.26)-(2.29) и требует в 3 раза меньше энергетических затрат. Кроме того данный способ синтеза управления применим к более широкому классу нелинейных систем, чем рассмотренная система (2.7).
