Решение многих технических задач методами теории графов сводятся к определению тех или иных характеристик графов. К важнейшим характеристикам графов относятся: цикломатическое число, хроматическое число, множество внутренней устойчивости, множество внешней устойчивости.
Цикломатическое число. Пусть G – неориентированный граф, имеющий п вершин, т ребер и r компонент связности. Цикломатическим числом графа G называется число:
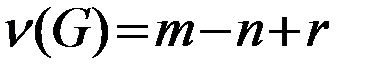 (4.7)
(4.7)
Это число имеет следующий смысл: оно равно наибольшему числу независимых циклов в графе.
Хроматическое число. Пусть р – натуральное число. Граф G называют р –хроматическим, если его вершины можно раскрасить р различными цветами так, чтобы никакие две смежные вершины не были раскрашены одинаково. Наименьшее число р, при котором граф является р – хроматическим, называется хроматическим числом и обозначают γ(G).
Если γ(G) = 2, то граф называется бихроматическим. Необходимым и достаточным условием того, чтобы граф был бихроматическим, является отсутствие в нем циклов нечетной длины. Хроматическое число, например, играет важную роль при решении задачи наиболее экономичного использования памяти при программировании. Однако его определение, за исключением случая бихроматического графа, представляет собой трудную задачу, требующую для своего решения компьютер.
Множество внутренней устойчивости. Множество 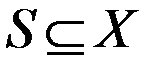 графа
графа 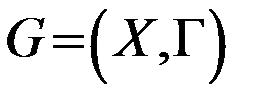 называется внутренне устойчивым, если никакие две вершины из S не смежны, т.е. для
называется внутренне устойчивым, если никакие две вершины из S не смежны, т.е. для 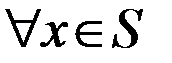 имеет место
имеет место 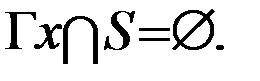
Множество внутренней устойчивости, содержащее наибольшее число элементов, называется наибольшим внутренним устойчивым множеством, а число элементов этого множества – числом внутренней устойчивости графа G.
Множество внешней устойчивости. Множество 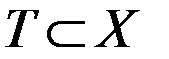 графа
графа 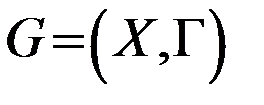 называется внешне устойчивым, если любая вершина, не принадлежащая Т, соединена дугами с вершинами из Т, т.е.
называется внешне устойчивым, если любая вершина, не принадлежащая Т, соединена дугами с вершинами из Т, т.е. 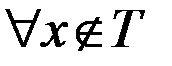 имеет место
имеет место 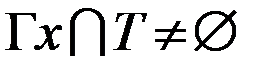 .
.
Множество внешней устойчивости, содержащее наименьшее число элементов, называется наименьшим внешние устойчивым множеством,, а число элементов этого множества - числом внешней устойчивости графа G.
Задача о кратчайшем пути
В практических приложениях имеет большое значение задача нахождения кратчайшего пути между двумя вершинами связного неориентированного графа. К такой задаче сводятся многие задачи выбора наиболее экономичного (с точки зрения расстояния или времени или стоимости) маршрута на имеющейся карте дорог; многие задачи выбора наиболее экономичного перевода динамической системы из одного состояния в другое и т.п. В математике разработан ряд методов решения подобных задач, однако методы, основанные на использовании графов, оказываются наименее трудоемкими.
Задача о кратчайшем пути на графе в общем виде может быть сформулирована следующим образом. Дан неориентированный граф 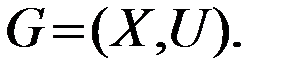 Каждому ребру этого графа приписано некоторое число l(u) ≥ 0, называемое длиной ребра. В частных случаях l(u) может между вершинами, соединяемыми ребром и, временем или стоимостью проезда по этому ребру и т.п. При этом любая цепь μ будет характеризоваться длиной, определяемой формулой
Каждому ребру этого графа приписано некоторое число l(u) ≥ 0, называемое длиной ребра. В частных случаях l(u) может между вершинами, соединяемыми ребром и, временем или стоимостью проезда по этому ребру и т.п. При этом любая цепь μ будет характеризоваться длиной, определяемой формулой 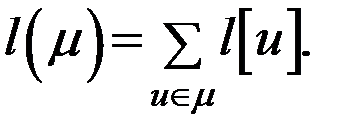
Требуется для произвольных вершин а и b графа G такой путь μab, который был бы наименьшим.
Прежде чем найти общий метод решения этой задачи, рассмотрим решение задачи частного вида, когда длина каждого ребра равна единице.
 2015-01-30
2015-01-30 1342
1342








