Определение

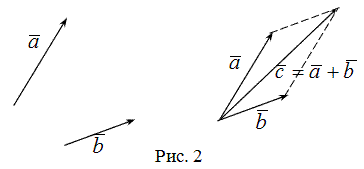
Правило параллелограмма - если два неколлинеарных вектора 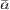и 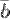привести к общему началу, то вектор совпадает с диагональю параллелограмма, построенного на векторах 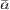и 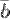(рис. 2). Причем начало вектора 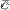совпадает с началом заданных векторов.

Вектор называется противоположным вектором к вектору 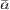, если он коллинеарен вектору 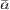, равен ему по длине, но направлен в противоположную сторону вектору .

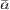Операция сложения векторов обладает следующими свойствами:

1. - коммутативность

2. - ассоциативность

3.

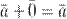
4.

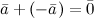
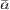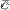Разностью векторов и называется вектор такой, что выполняется условие: (рис. 3).

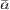Произведением вектора на число 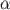называется вектор 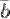, удовлетворяющий условиям:

1.

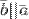
2.

3. , если 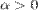, , 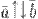если .

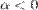Свойства умножения вектора на число:

1.

2.

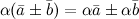
3.

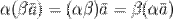
4.

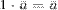
5.

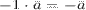
6.