Задача 1. Имеются данные по сдаче сессии в двух группах Балл Число учащихся 1 группа 2 группа 1-3 4-6 7-9

Имеются данные по сдаче сессии в двух группах

Рассчитать средний балл успеваемости по каждой группе. Определите, в какой группе успеваемость ниже, устойчивее.

Решение:

Средний балл успеваемости определяем по средней арифметической взвешенной:

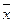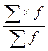= так как

Осредняемый признак (балл) дан в виде интервала – определяем середину каждого из интервалов, тогда:

Средний балл успеваемости по первой группе:

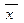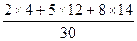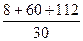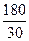= = = = 6,0;

Средний балл успеваемости по второй группе:

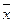
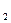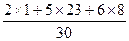= = = = 5,5.

Успеваемость выше в первой группе, но чтобы охарактеризовать, где успеваемость более устойчивее рассчитаем показатели вариации (колебания):

Средний квадрат отклонения и коэффициент вариации.

Средний квадрат отклонения (дисперсия) по первой группе:

= ;

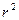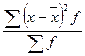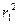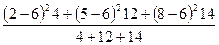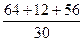= = = 4,4;

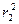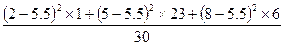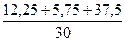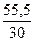= = = = 1,85.

Коэффициент вариации характеризует отклонение в процентах:

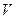
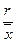= • 100%;

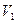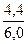= • 100% = 7,3%;

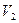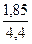= • 100% = 4,2%.

Средний балл успеваемости выше в первой группе, однако, устойчивее успеваемость (однороднее) во второй, так как показатель вариации (колебания) успеваемости во второй группе ниже.

ТЕМА: «Ряды динамики»