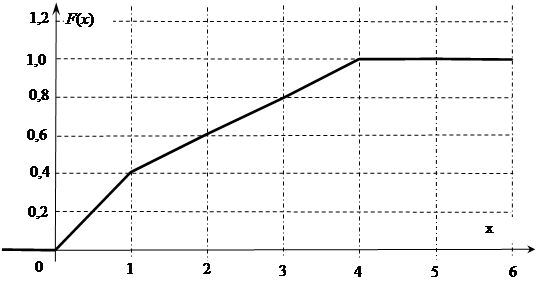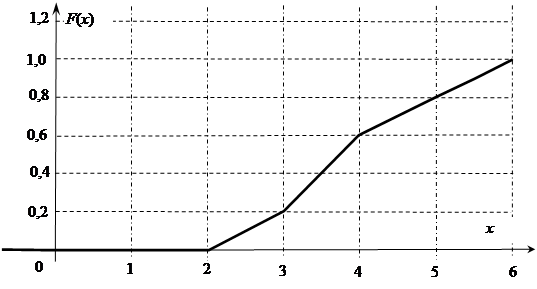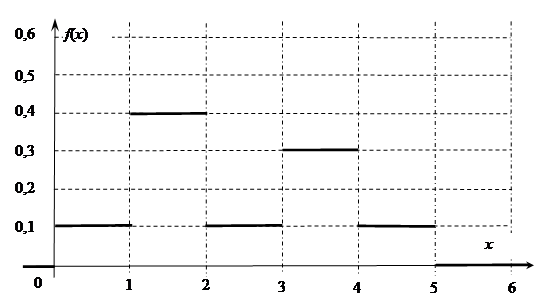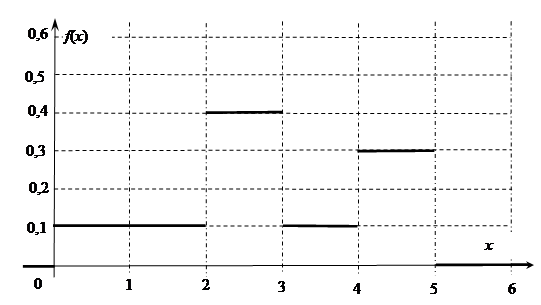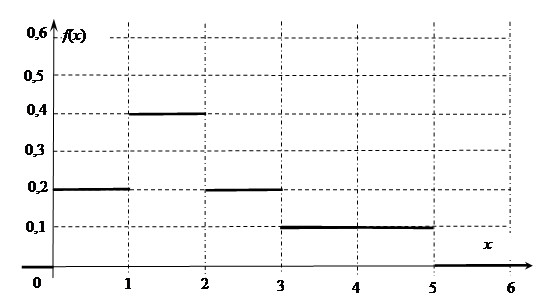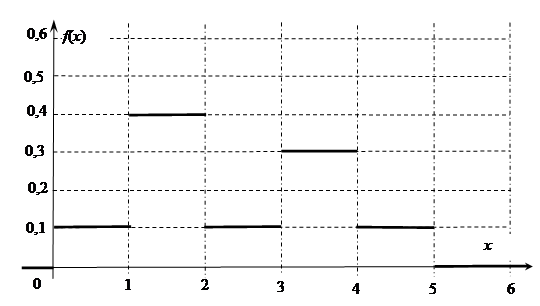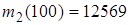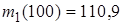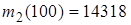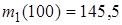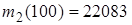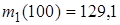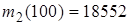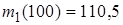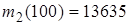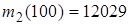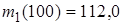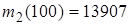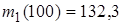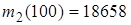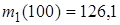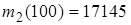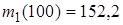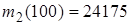КР №1 «Теория вероятностей и математическая статистика»
(1-10) Вероятности четырех независимых в совокупности событий 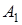 ,
,  ,
, 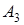 ,
, 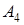 соответственно равны
соответственно равны 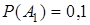 ;
; 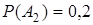 ;
; 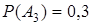 и
и 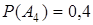 . События
. События 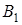 и
и 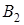 заданы с помощью словесного описания. Используя операции алгебры событий, выразите события
заданы с помощью словесного описания. Используя операции алгебры событий, выразите события 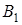 и
и 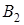 через
через 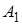 ,
,  ,
, 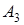 ,
, 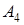 . Найдите вероятности событий
. Найдите вероятности событий 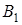 и
и 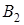 .
.
| Номер задачи
| Событие 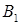
| Событие 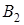
|
| 1.
| Произойдет хотя бы одно из четырех событий.
| Произойдет только одно из четырех событий.
|
| 2.
| Произойдёт событие 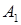 и не произойдёт хотя бы одно из остальных событий. и не произойдёт хотя бы одно из остальных событий.
| Произойдёт только событие 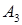 или только событие или только событие 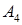 из данных четырёх событий. из данных четырёх событий.
|
| 3.
| Произойдет только одно из событий 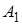 , ,  , , 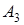 и событие и событие 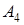 . .
| Не произойдет хотя бы одного из событий 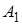 , ,  , , 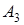 , , 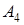 . .
|
| 4.
| Не произойдёт хотя бы одно из событий  , , 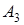 , , 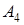 . .
| Не произойдёт или событие 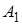 или событие или событие 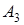 . .
|
| 5.
| Не произойдет ни одно из четырех событий
| Хотя бы одно из четырёх событий не произойдёт.
|
| 6.
| Одно из четырех событий не произойдет, а остальные три события произойдут
| Произойдёт событие 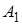 или не произойдёт событие или не произойдёт событие 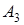 . .
|
| 7.
| Не произойдут только  и и 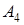 . .
| Не произойдут  или или 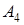 . .
|
| 8.
| Произойдут только  и и 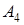 . .
| Не произойдет только одно из этих четырех событий
|
| 9.
| Произойдёт только событие  или только событие или только событие 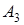 . .
| Не произойдёт ни событие 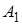 , ни событие , ни событие  . .
|
| 10.
| Произойдёт событие 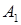 или не произойдёт ни одно из четырёх событий. или не произойдёт ни одно из четырёх событий.
| Произойдёт событие 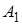 или хотя бы одно из событий или хотя бы одно из событий  , , 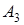 и и 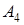 . .
|
(11-20). Вероятность попадания стрелком в мишень равна 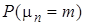 Найти вероятность того, что спортсмен поразит мишень ровно
Найти вероятность того, что спортсмен поразит мишень ровно 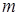 раз в
раз в 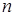 выстрелах, если вероятность попадания при одном выстреле равна
выстрелах, если вероятность попадания при одном выстреле равна 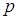 .
.
| Номер задачи
|
|
|
|
|
|
|
|
|
|
|
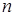
|
|
|
|
|
|
|
|
|
|
|
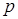
| 0,9
| 0,8
| 0,5
| 0,7
| 0,6
| 0,8
| 0,6
| 0,3
| 0,9
| 0,5
|
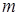
|
|
|
|
|
|
|
|
|
|
|
(21-30) Из урны, содержащей 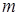 белых и
белых и 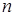 черных шаров случайным образом вынимают 2 шара. Найти вероятности следующих событий:
черных шаров случайным образом вынимают 2 шара. Найти вероятности следующих событий:
a. оба шара белые;
b. оба шара черные;
c. шары разных цветов.
| Номер задачи
|
|
|
|
|
|
|
|
|
|
|
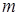
|
|
|
|
|
|
|
|
|
|
|
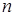
|
|
|
|
|
|
|
|
|
|
|
(31-40) В последовательности испытаний по схеме Бернулли известна вероятность успеха 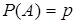 . Найти следующие вероятности
. Найти следующие вероятности 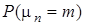 ,
, 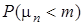 ,
, 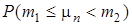 , где
, где 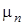 – число успехов в последовательности из
– число успехов в последовательности из 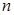 испытаний.
испытаний.
| Номер задачи
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
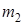
|
|
|
|
|
|
|
|
|
|
|
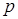
| 0,5
| 0,4
| 0,6
| 0,5
| 0,4
| 0,6
| 0,5
| 0,4
| 0,6
| 0,4
|
(41-50) Дискретная случайная величина 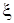 , принимающая значения
, принимающая значения 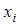 (
(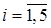 ), задана таблицей распределения.
), задана таблицей распределения.
Постройте функцию распределения 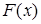 случайной величины
случайной величины 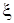 , найдите математическое ожидание
, найдите математическое ожидание 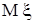 , дисперсию
, дисперсию 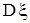 , вероятность события
, вероятность события 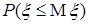 .
.
| Номер задачи
|
|
|
|
|
|
|
|
|
|
|

| 0,2
| 0,1
| 0,4
| 0,1
| 0,1
| 0,1
| 0,4
| 0,3
| 0,1
| 0,2
|
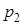
| 0.4
| 0,3
| 0,1
| 0,3
| 0,4
| 0,1
| 0,1
| 0,1
| 0,1
| 0,1
|
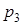
| 0,2
| 0,4
| 0,2
| 0,1
| 0,1
| 0,4
| 0,1
| 0,2
| 0,1
| 0,2
|
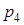
| 0,1
| 0,1
| 0,2
| 0,1
| 0,3
| 0,1
| 0,2
| 0,1
| 0,3
| 0,1
|
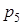
| 0,1
| 0,1
| 0,1
| 0,4
| 0,1
| 0,3
| 0,2
| 0,3
| 0,4
| 0,4
|
(51-60) Функция распределения 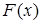 случайной величины
случайной величины 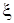 задана графически. Постройте график плотности распределения
задана графически. Постройте график плотности распределения 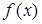 данной случайной величины и найдите указанные вероятности.
данной случайной величины и найдите указанные вероятности.
(61-70) Функция плотности 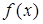 случайной величины
случайной величины 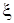 задана графически. Найти математическое ожидание этой случайной величины
задана графически. Найти математическое ожидание этой случайной величины 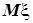 и указанные вероятности.
и указанные вероятности.
| 65.
|
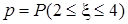
|
| 66.
|
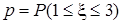
|
| 69.
|
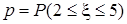
|
| 70.
|
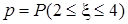
|
(71-80) Случайная величина 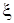 , распределена по нормальному закону с параметрами
, распределена по нормальному закону с параметрами 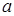 и
и 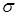 . Найти вероятности событий:
. Найти вероятности событий: 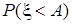 ;
; 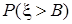 ;
; 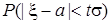 .
.
| Номер задачи
|
|
|
|
|
|
|
|
|
|
|
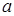
|
|
|
|
|
|
|
|
|
|
|
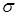
|
|
|
|
|
|
|
|
|
|
|
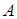
|
|
|
|
|
|
|
|
|
|
|
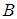
|
|
|
|
|
|
|
|
|
|
|
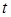
| 1,5
| 0,5
| 1,0
| 2,0
| 1,5
| 2,0
| 1,0
| 0,5
| 1,5
| 1,0
|
(81-90) В таблицах представлены данные о технико-экономическом показателе 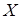 , собранные на одной из дорог ОАО «РЖД» за 2010. В результате первичной обработки данных построен вариационный ряд, проведена группировка, найдены
, собранные на одной из дорог ОАО «РЖД» за 2010. В результате первичной обработки данных построен вариационный ряд, проведена группировка, найдены 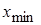 ,
, 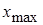 (наименьший и наибольший элементы выборки
(наименьший и наибольший элементы выборки 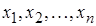 из генеральной совокупности
из генеральной совокупности 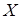 ), а также выборочные начальные моменты
), а также выборочные начальные моменты
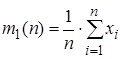 ,
, 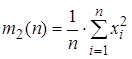 ,
, 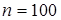 .
.
Результаты группировки сведены в таблицу, в которой 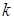 – число интервалов разбиения отрезка
– число интервалов разбиения отрезка 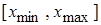 ,
, 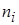 – число точек, попавших в i -й интервал
– число точек, попавших в i -й интервал 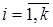 .
.
a. Найти размах исходной выборки и числа 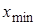 ,
, 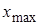 .
.
b. Найти выборочные моменты для выборки, составленной из первых 10 элементов исходной выборки, то есть числа 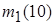 ,
, 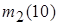 .
.
c. По группированной выборке построить гистограмму относительных частот, найти выборочное среднее 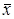 и выборочную дисперсию
и выборочную дисперсию 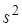 .
.
d. Сравнить числа 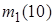 ,
, 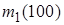 ,
, 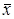 и объяснить их различие.
и объяснить их различие.
e. Сравнить гистограмму относительных частот с функцией плотности нормально распределённой случайной величины с параметрами 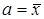 ,
, 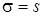 . Сделать вывод о нормальности генеральной совокупности
. Сделать вывод о нормальности генеральной совокупности 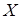 , из которой сделана исходная выборка.
, из которой сделана исходная выборка.
| 81. Объем перевозок гипса Восточно-Сибирской дороги (в тоннах).
|
|
| | Результаты первичной обработки
| | Номера интервалов
| Границы интервалов разбиения
| Частоты 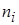
| |
| 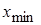
| 61,83
|
| |
| 61,83
| 103,67
|
| |
| 103,67
| 145,5
|
| |
| 145,5
| 187,33
|
| |
| 187,33
| 229,17
|
| |
| 229,17
| 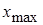
|
| 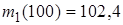
| 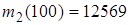
|
|
| 82. Объем перевозки щебня Горьковской дорогой (в тоннах).
|
|
| | Результаты первичной обработки
| | Номера интервалов
| Границы интервалов разбиения
| Частоты 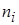
| |
| 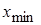
| 53,14
|
| |
| 53,14
| 101,29
|
| |
| 101,29
| 149,43
|
| |
| 149,43
| 197,57
|
| |
| 197,57
| 245,71
|
| |
| 245,71
| 293,86
|
| |
| 293,86
| 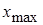
|
| 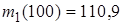
| 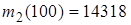
|
|
| 83. Объем перевозки щебня Западно-Сибирской дорогой (в тоннах).
|
|
| | Результаты первичной обработки
| | Номера интервалов
| Границы интервалов разбиения
| Частоты 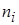
| |
| 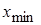
| 81,14
|
| |
| 81,14
| 100,29
|
| |
| 100,29
| 119,43
|
| |
| 119,43
| 138,57
|
| |
| 138,57
| 157,71
|
| |
| 157,71
| 176,86
|
| |
| 176,86
| 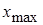
|
| 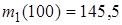
| 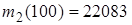
|
|
| 84. Объем перевозки песка Горьковской дорогой (в тоннах).
|
|
| | Результаты первичной обработки
| | Номера интервалов
| Границы интервалов разбиения
| Частоты 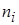
| |
| 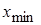
| 70,43
|
| |
| 70,43
| 91,86
|
| |
| 91,86
| 113,29
|
| |
| 113,29
| 134,71
|
| |
| 134,71
| 156,14
|
| |
| 156,14
| 177,57
|
| |
| 177,57
| 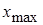
|
| 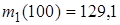
| 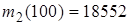
|
|
| 85. Объем перевозки щебня Дальневосточной дорогой (в тоннах).
|
|
| | Результаты первичной обработки
| | Номера интервалов
| Границы интервалов разбиения
| Частоты 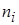
| |
| 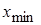
| 81,71
|
| |
| 81,71
| 102,43
|
| |
| 102,43
| 123,14
|
| |
| 123,14
| 143,86
|
| |
| 143,86
| 164,57
|
| |
| 164,57
| 185,29
|
| |
| 185,29
| 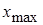
|
| 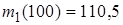
| 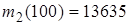
|
|
| 86.. Объем перевозки песка Дальневосточной дорогой (в тоннах).
|
|
| | Результаты первичной обработки
| | Номера интервалов
| Границы интервалов разбиения
| Частоты 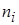
| |
| 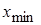
| 38,75
|
| |
| 38,75
| 62,5
|
| |
| 62,5
| 86,25
|
| |
| 86,25
|
|
| |
|
| 133,75
|
| |
| 133,75
| 157,5
|
| |
| 157,5
| 181,25
|
| |
| 181,25
| 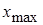
|
| 
| 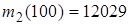
|
|
| 87. Объем перевозки порошка минерального Дальневосточной дорогой (в тоннах).
|
|
| | Результаты первичной обработки
| | Номера интервалов
| Границы интервалов разбиения
| Частоты 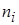
| |
| 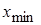
| 85,33
|
| |
| 85,33
| 105,67
|
| |
| 105,67
|
|
| |
|
| 146,33
|
| |
| 146,33
| 166,67
|
| |
| 166,67
| 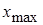
|
| 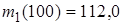
| 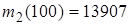
|
|
| 88. Объем перевозки щебня Забайкальской дорогой (в тоннах).
|
|
| | Результаты первичной обработки
| | Номера интервалов
| Границы интервалов разбиения
| Частоты 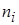
| |
| 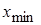
| 83,43
|
| |
| 83,43
| 101,86
|
| |
| 101,86
| 120,29
|
| |
| 120,29
| 138,71
|
| |
| 138,71
| 157,14
|
| |
| 157,14
| 175,57
|
| |
| 175,57
| 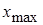
|
| 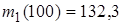
| 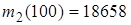
|
|
| 89. Объем перевозки песка Западно-Сибирской дорогой (в тоннах).
|
|
| | Результаты первичной обработки
| | Номера интервалов
| Границы интервалов разбиения
| Частоты 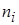
| |
| 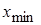
| 85,71
|
| |
| 85,71
| 104,43
|
| |
| 104,43
| 123,14
|
| |
| 123,14
| 141,86
|
| |
| 141,86
| 160,57
|
| |
| 160,57
| 179,29
|
| |
| 179,29
| 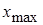
|
| 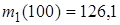
| 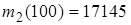
|
|
| 90.Объем перевозки щебня Московской дорогой (в тоннах).
|
|
| | Результаты первичной обработки
| | Номера интервалов
| Границы интервалов разбиения
| Частоты 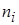
| |
| 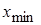
| 85,71
|
| |
| 85,71
| 104,43
|
| |
| 104,43
| 123,14
|
| |
| 123,14
| 141,86
|
| |
| 141,86
| 160,57
|
| |
| 160,57
| 179,29
|
| |
| 179,29
| 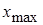
|
| 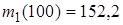
| 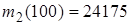
|
|
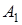 ,
,  ,
, 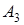 ,
, 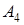 соответственно равны
соответственно равны 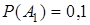 ;
; 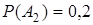 ;
; 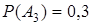 и
и 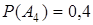 . События
. События 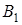 и
и 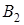 заданы с помощью словесного описания. Используя операции алгебры событий, выразите события
заданы с помощью словесного описания. Используя операции алгебры событий, выразите события 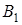 и
и 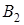 через
через 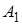 ,
,  ,
, 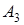 ,
, 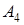 . Найдите вероятности событий
. Найдите вероятности событий 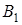 и
и 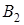 .
.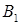
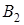
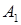 и не произойдёт хотя бы одно из остальных событий.
и не произойдёт хотя бы одно из остальных событий.
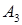 или только событие
или только событие 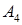 из данных четырёх событий.
из данных четырёх событий.
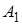 ,
,  ,
, 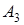 и событие
и событие 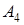 .
.
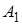 ,
,  ,
, 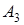 ,
, 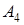 .
.
 ,
, 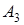 ,
, 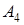 .
.
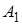 или событие
или событие 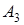 .
.
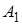 или не произойдёт событие
или не произойдёт событие 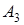 .
.
 и
и 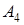 .
.
 или
или 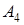 .
.
 и
и 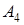 .
.
 или только событие
или только событие 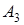 .
.
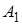 , ни событие
, ни событие  .
.
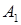 или не произойдёт ни одно из четырёх событий.
или не произойдёт ни одно из четырёх событий.
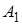 или хотя бы одно из событий
или хотя бы одно из событий  ,
, 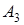 и
и 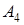 .
.
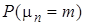 Найти вероятность того, что спортсмен поразит мишень ровно
Найти вероятность того, что спортсмен поразит мишень ровно 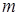 раз в
раз в 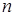 выстрелах, если вероятность попадания при одном выстреле равна
выстрелах, если вероятность попадания при одном выстреле равна 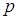 .
.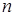
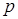
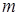
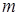 белых и
белых и 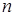 черных шаров случайным образом вынимают 2 шара. Найти вероятности следующих событий:
черных шаров случайным образом вынимают 2 шара. Найти вероятности следующих событий: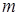
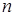
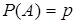 . Найти следующие вероятности
. Найти следующие вероятности 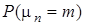 ,
, 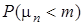 ,
, 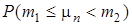 , где
, где 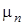 – число успехов в последовательности из
– число успехов в последовательности из 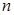 испытаний.
испытаний.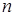
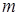
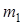
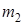
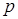
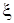 , принимающая значения
, принимающая значения 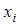 (
(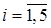 ), задана таблицей распределения.
), задана таблицей распределения.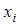
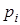

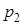
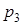
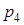
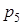
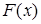 случайной величины
случайной величины 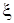 , найдите математическое ожидание
, найдите математическое ожидание 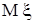 , дисперсию
, дисперсию 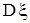 , вероятность события
, вероятность события 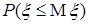 .
.
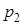
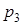
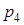
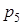
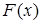 случайной величины
случайной величины 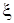 задана графически. Постройте график плотности распределения
задана графически. Постройте график плотности распределения 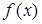 данной случайной величины и найдите указанные вероятности.
данной случайной величины и найдите указанные вероятности.
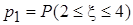 ;
; 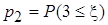 ,
, 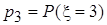 .
.
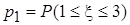 ;
; 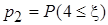
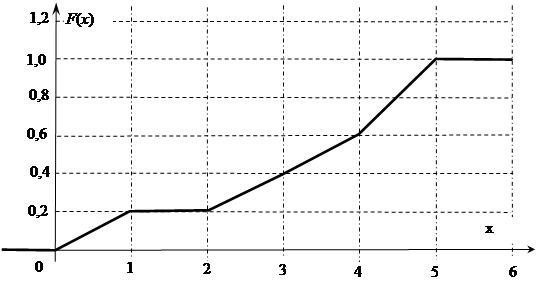 ;
; 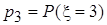 .
.
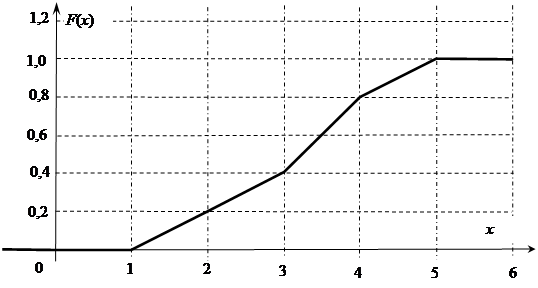
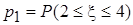 ;
; 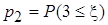 ;
; 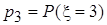 .
.
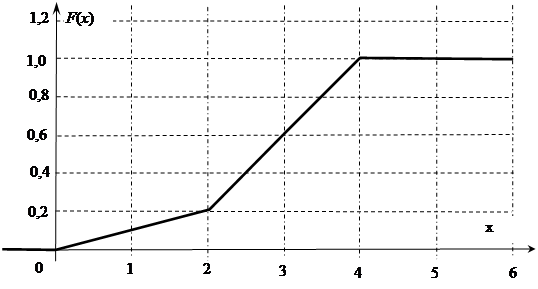
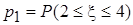 ;
; 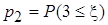 ;
; 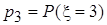 .
.
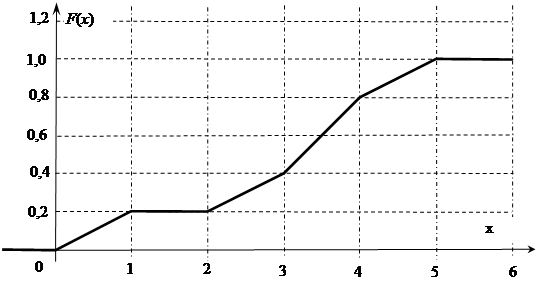
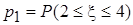 ;
; 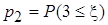 ,
, 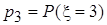 .
.
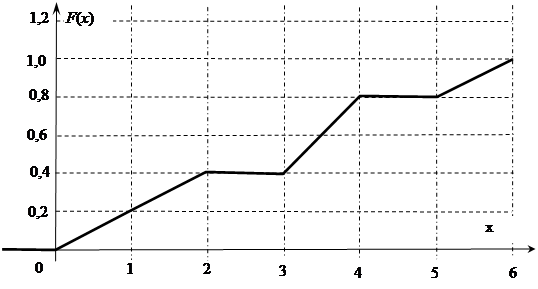
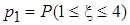 ;
; 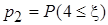 ;
; 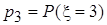 .
.
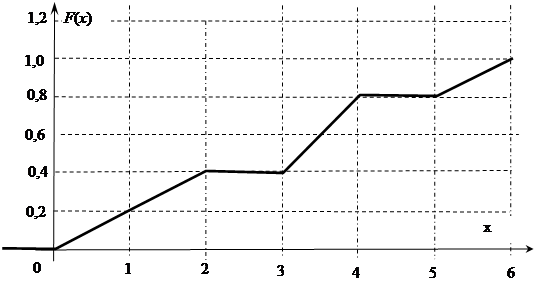
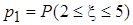 ;
; 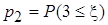 ;
; 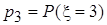 .
.
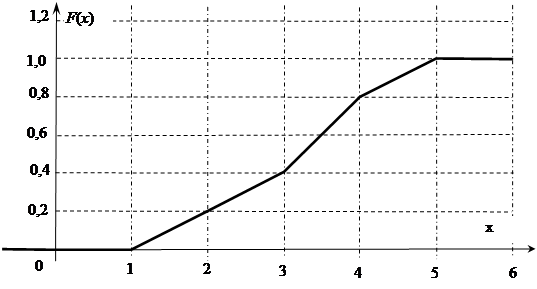
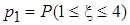 ;
; 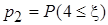 ;
; 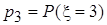 .
.
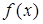 случайной величины
случайной величины 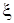 задана графически. Найти математическое ожидание этой случайной величины
задана графически. Найти математическое ожидание этой случайной величины 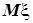 и указанные вероятности.
и указанные вероятности.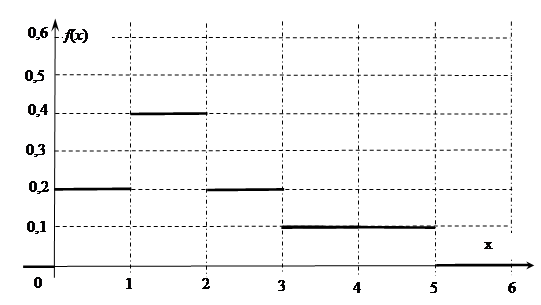
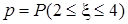
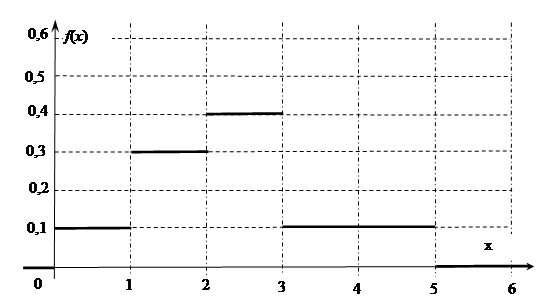
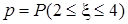
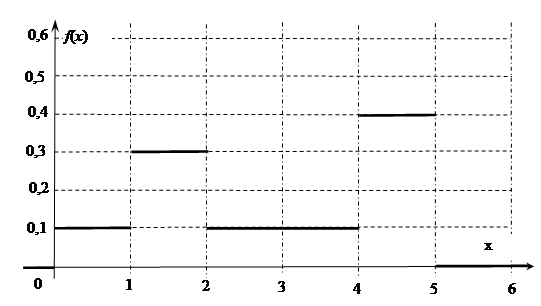
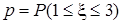
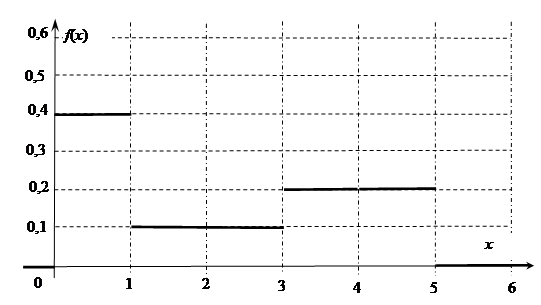
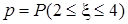
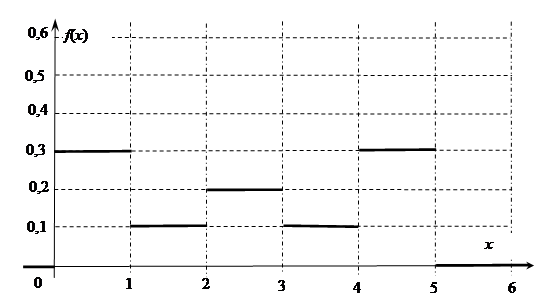
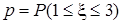
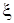 , распределена по нормальному закону с параметрами
, распределена по нормальному закону с параметрами 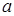 и
и 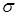 . Найти вероятности событий:
. Найти вероятности событий: 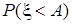 ;
; 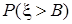 ;
; 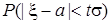 .
.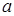
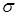
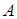
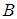
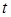
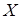 , собранные на одной из дорог ОАО «РЖД» за 2010. В результате первичной обработки данных построен вариационный ряд, проведена группировка, найдены
, собранные на одной из дорог ОАО «РЖД» за 2010. В результате первичной обработки данных построен вариационный ряд, проведена группировка, найдены 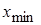 ,
, 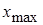 (наименьший и наибольший элементы выборки
(наименьший и наибольший элементы выборки 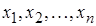 из генеральной совокупности
из генеральной совокупности 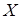 ), а также выборочные начальные моменты
), а также выборочные начальные моменты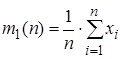 ,
, 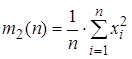 ,
, 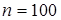 .
.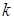 – число интервалов разбиения отрезка
– число интервалов разбиения отрезка 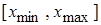 ,
, 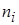 – число точек, попавших в i -й интервал
– число точек, попавших в i -й интервал 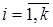 .
.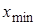 ,
, 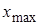 .
.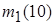 ,
, 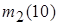 .
.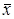 и выборочную дисперсию
и выборочную дисперсию 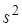 .
.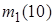 ,
, 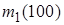 ,
, 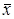 и объяснить их различие.
и объяснить их различие.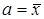 ,
, 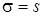 . Сделать вывод о нормальности генеральной совокупности
. Сделать вывод о нормальности генеральной совокупности 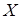 , из которой сделана исходная выборка.
, из которой сделана исходная выборка. 2015-01-30
2015-01-30 802
802