Пусть А – конечное множество. Через ½А½ обозначим число элементов множества А, иначе называемое мощностью множества А.
Закон аддитивности. Если множества А и В не имеют общих элементов, то ½АÈВ½=½А½+½В½
Задача 1. В классе 12 мальчиков и 14 девочек. Сколько всего учеников в классе?
Эта задача показывает, что закон аддитивности мы знаем давно и пользуемся этим законом с первого класса, а то и раньше.
Задача 2. Все ученики в классе обязаны посещать хотя бы один из двух кружков: по физике или по математике. Математический кружок посещают 16 человек, физический – 14. Сколько всего человек в классе?
Для решения этой задачи закон аддитивности не применим, поскольку рассматриваемые в ней множества могут иметь непустое пересечение. Для нахождения точного числа учеников в классе нужно знать, сколько человек посещают оба кружка. При отсутствии этой информации общее число учеников может меняться от 16 до 30.
Следствия из закона аддитивности.
Следствие 1. Если ВÌА, то ½А½=½В½+½А\В½.
Следствие 2. ½А½=½АÇВ½+½А\В½
Следствие 3. |АÈВ|=|А|+|В|–|АÇВ|.
Задача 3. Все ученики в классе обязаны посещать хотя бы один из двух кружков: по физике или по математике. Математический кружок посещают 16 человек, физический – 14. Оба кружка посещают 4 человека. Сколько всего человек в классе?
Задача 4. Докажите следствия 1–3. Укажите, где в доказательстве использован закон аддитивности.
Задача 5. Сколько существует натуральных чисел, не превосходящих 1000, которые делятся и на 3 и на 5?
Задача 6. Сколько существует натуральных чисел, не превосходящих 1000, которые делятся хотя бы на одно из чисел 3 и 5?
Задача 7. Сколько существует натуральных чисел, не превосходящих числа а = 35×53 и взаимно простых с а?
Задача 8. Сколько существует натуральных чисел, не превосходящих 1000, которые делятся на 3, но не делятся на 5?
Задача 9. Пусть уравнение f(x)=0 имеет n решений, уравнение g(x)=0 имеет m решений, а система 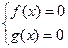 имеет k решений. Сколько решений имеет уравнение f(x)×g(x)=0 при условии, что оба уравнения определены при всех значениях х?
имеет k решений. Сколько решений имеет уравнение f(x)×g(x)=0 при условии, что оба уравнения определены при всех значениях х?
Задача 10. Каждый из учеников класса ходил хотя бы в один из двух походов, причем в каждом из этих походов девочек было не больше 40% от общего числа участников. Докажите, что в классе не более 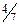 девочек.
девочек.
Закон аддитивности справедлив не только при подсчете количества элементов конечных множеств. Этому же закону подчиняются длины отрезков (и других множеств на прямой), площади фигур на плоскости, объемы тел в трехмерном пространстве. Многие физические величины также подчиняются закону аддитивности.
Задача 11. На отрезке единичной длины расположено несколько непересекающихся отрезков, обладающих свойством: на этих отрезках нельзя найти двух точек, расстояние между которыми равно 0,5. Докажите, что суммарная длина данных отрезков не превосходит 0,5.
Закон мультипликативности (правило умножения). Число всевозможных пар вида (a,b), где а – элемент множества А, а b – элемент множества В, равно ½А½´½В½.
Задача 12. В классе 12 мальчиков и 15 девочек. Для участия в конкурсе нужно выбрать одного мальчика и одну девочку. Сколькими способами это можно сделать?
Задача 13. Пусть уравнение f(x)=0 имеет n решений, а уравнение g(y)=0 имеет m решений. Сколько решений имеет система 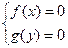 ?
?
Задача 14. Сколько различных натуральных делителей имеет число 2n×3m?
Задача 15. Докажите, что число обладает нечетным количеством различных натуральных делителей тогда и только тогда, когда оно является полным квадратом.
Задача 16. В условиях задачи 3 определить, сколькими способами можно выбрать для выступления в математической и физической олимпиадах по одному участнику соответствующего кружка при условии, что две эти олимпиады проходят одновременно.
Для решения этой задачи правило умножения нельзя применять непосредственно. Действительно, это правило не исключает из рассмотрения пары вида (а,а), появляющиеся в том случае, когда множества А и В имеют непустое пересечение. Однако по смыслу задачи нас не устраивают такие пары, так как один ученик не может участвовать в двух олимпиадах одновременно. То есть из общего количества пар, равного 16×14, надо вычесть 4 пары вида (а,а).
Задача 17. Пусть |А|=n, |В|=m, |АÇВ|=k. Сколько существует пар вида (a,b), где а – элемент множества А, а b – элемент множества В, причем a¹b.
Задача 18. Пусть |А|=n. Сколько существует пар вида (a,b), где а и b – элементы множества А, причем a¹b.
Задача 19. В классе 27 человек. Сколькими способами из них можно выбрать старосту и заместителя старосты?
Эту задачу решается тем же способом, что и предыдущие две – из общего количества пар вычитаются 27 пар вида (а,а). Однако можно рассуждать по другому: старосту класса можно выбрать 27 способами, его заместителя – 26 способами; всего получается 27×26 способов.
Сформулируем правило, позволяющее решать подобные задачи.
Пускай первый элемент пары можно выбрать n способами, а второй – m способами. Тогда общее количество пар равно n´m.
Задача 20. Сколькими способами можно поставить на шахматную доску черную и белую ладьи так, чтобы они не били друг друга.
Задача 21. В классе 27 человек. Сколькими способами из них можно выбрать старосту, помощника старосты и заместителя старосты?
Задача 22. В классе 27 человек. Сколькими способами из них можно выбрать двух человек для дежурства в столовой?
Почувствуйте разницу между задачами 19 и 22. В задаче 19 из двух учеников можно образовать две пары, поскольку не все равно, кто именно будет старостой, а кто его заместителем. В задаче 22 из двух учеников можно образовать только одну пару – поэтому общее количество пар в этой задаче в два раза меньше.
Задача 23. В шахматном турнире, проводимом по круговой системе (каждый участник встречается с каждым по одному разу), играет 12 человек. Сколько всего партий должно быть сыграно в этом турнире.
Задача 24. На плоскости расположено 10 точек. Сколько существует отрезков с концами в этих точках?
Задача 25. Сколько диагоналей у выпуклого n-угольника?
Задача 26. В классе 8 девочек и 17 мальчиков. Сколькими способами из их числа можно выбрать двух девочек и одного мальчика?
Задача 27. В классе 27 человек. Для участия в физической, химической и математической олимпиадах необходимо выбрать трех разных учеников. Сколькими способами это можно сделать?
Задача 28. Сколько различных натуральных делителей имеет число 2n×3m×5k?
Для решения трех последних задач (а также задачи 21) правило умножения нужно применить дважды. Поскольку подобная ситуация возникает довольно часто, имеет смысл сформулировать правило умножения в следующем, более общем, виде:
Пусть нам нужно составить набор из n предметов, причем первый предмет можно выбрать к1 способами, второй предмет – к2 способами и т.д. Тогда общее количество всевозможных наборов равно к1×к2×к3×…×кn..
Задача 29. Сколькими способами пять учеников можно построить в шеренгу?
Задача 30. Сколькими способами пять учеников можно построить в шеренгу, если Вова не должен стоять первым?
Заметим, что при решении этой задачи можно рассуждать по разному. Первый способ: на первое место можно поставить одного из 4 детей (любого кроме Вовы), на второе – одного из 4 (трое оставшихся и Вова), на третье – одного из трех, на четвертое – одного из двух, на пятое место автоматически попадает оставшийся ученик; всего получается 4×4×3×2=96 вариантов. Второй способ: Вову можно поставить на одно из 4 мест, Петю – на одно из 4, Машу – на одно из трех, Марину – на одно из двух. Можно рассуждать и так: из общего количества способов (Вова стоит где угодно) вычесть количество способов, при которых Вова стоит на первом месте (таких способов 4×3×2=24).
Задача 31. Сколькими способами пять учеников можно построить в шеренгу, если Вова не должен стоять с краю?
Задача 32. Сколькими способами n учеников можно построить в шеренгу?
Задача 33. Сколько анаграмм можно составить из букв слова ПТИЦА?
Задача 34. Сколько анаграмм можно составить из букв слова ПИЦЦА?
Задача 35. Сколько существует шестизначных чисел, в десятичной записи которых использованы только цифры 1, 2, 3, 4, 5?
Задача 36. Сколько существует шестизначных чисел, в десятичной записи которых использованы только цифры 0, 1, 2, 3, 4?
Задача 37. Сколько существует шестизначных чисел, в десятичной записи которых каждая цифра встречается не более одного раза?
Очень часто для решения одной задачи приходится применять как правило умножения, так и правило сложения. Обычно это происходит по следующей схеме: множество А разбивается на подмножества Аi таким образом, что число элементов каждого из них можно определить по правилу умножения.
Задача 38. Сколькими способами можно поставить на шахматную доску черного и белого королей так, чтобы они не били друг друга.
Задача 39. Сколькими способами можно построить в шеренгу пять учеников, если Ваня и Маша обязательно хотят стоять рядом?
Задача 40. Сколько можно составить из букв слова ПИЦЦА таких анаграмм, в которых две буквы Ц не стоят рядом?
Задача 41. Сколько можно составить из букв слова КОМЕТА таких анаграмм, в которых гласные и согласные буквы чередуются?
Задача 42. Сколькими способами можно посадить за круглым столом 6 человек?
Мы рассмотрели ряд задач, решение которых основано на применении правил умножения и сложения. Попытаемся теперь как-то систематизировать подобные задачи. Большинство из них воспроизводит следующую ситуацию: из данных предметов необходимо по определенному принципу выбрать несколько штук. Набор выбираемых предметов принято называть выборкой. Множество, из которого выбираются предметы – выборочным множеством. Количество выбираемых предметов – размером (или объемом) выборки. Рассматриваются упорядоченные и неупорядоченные выборки. Неупорядоченные выборки характеризуются только своим составом, упорядоченные – составом выборки и порядком следования ее элементов (первый, второй, третий и т.д.). Кроме того, выборки подразделяются на две группы в зависимости от того, допускается ли в них выбор одного и того же предмета несколько раз (выборки с повторениями) или не допускается (выборки без повторений). Таким образом, имеется четыре вида выборок: упорядоченные с повторениями, упорядоченные без повторений, неупорядоченные с повторениями, неупорядоченные без повторений. Упорядоченные выборки называются иначе размещениями, а неупорядоченные – сочетаниями. При этом, когда говорят просто «сочетание», имеют в виду сочетание без повторений, в противном случае говорят «сочетание с повторениями». То же самое касается и размещений. Сочетание – это просто подмножество выборочного множества. Чтобы задать сочетание, надо перечислить входящие в это подмножество элементы, записав их в фигурные скобки: 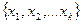 . Размещение – это упорядоченный набор элементов выборочного множества, его принято записывать в круглых скобках. Таким образом, к примеру, две записи
. Размещение – это упорядоченный набор элементов выборочного множества, его принято записывать в круглых скобках. Таким образом, к примеру, две записи 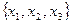 и
и 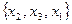 означают одно и то же сочетание, а записи (x1,x2,x3) и (x2,x3,x1) – два разных размещения. При решении задач очень важно бывает понять, какой вид выборки рассматривается в данной задаче. Так, если речь идет о трех участниках математической, физической и химической олимпиад, то мы имеем дело с упорядоченной выборкой (нам не все равно, кто в какой олимпиаде выступает). Если же в задаче говорится о трех участницах конкурса красоты, то выборка является неупорядоченной. Если три олимпиады происходят в одно время, и выступать в них должны разные ученики, то это выборка без повторений. Если же допускается выступление одного и того же ученика в разных олимпиадах, то выборка с повторениями.
означают одно и то же сочетание, а записи (x1,x2,x3) и (x2,x3,x1) – два разных размещения. При решении задач очень важно бывает понять, какой вид выборки рассматривается в данной задаче. Так, если речь идет о трех участниках математической, физической и химической олимпиад, то мы имеем дело с упорядоченной выборкой (нам не все равно, кто в какой олимпиаде выступает). Если же в задаче говорится о трех участницах конкурса красоты, то выборка является неупорядоченной. Если три олимпиады происходят в одно время, и выступать в них должны разные ученики, то это выборка без повторений. Если же допускается выступление одного и того же ученика в разных олимпиадах, то выборка с повторениями.
Задача 43. Для данных ситуаций определите выборочное множество. Найдите тип и размер выборки:
а) 10 разных предметов нужно разложить по трем разным ящикам;
б) имеется 10 разных ящиков; три разных предмета нужно убрать в эти ящики, не более одного предмета в ящик;
в) учитель задал Ване 10 задачек; Ваня решил сделать 3 из них, сказав, что остальные у него не получились;
г) у Маши в холодильнике лежат яблоки, груши и апельсины; Маша решила взять в школу 10 фруктов.
Задача 44. На танцплощадке собралось 8 юношей и 8 девушек. Сколькими способами их можно разбить на пары для участия в очередном танце?
Любая выборка характеризуется не только своим типом и размером, но и мощностью выборочного множества. В этом плане принято говорить о выборке из n по k, где n – число элементов выборочного множества, а k – размер выборки. Так, говорят о сочетаниях из n по k, о размещениях из n по k, о сочетаниях с повторениями из n по k и о размещениях с повторениями из n по k. При этом число сочетаний из n по k обозначают 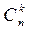 , число размещений из n по k обозначают
, число размещений из n по k обозначают 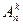 . Соответственно число сочетаний и размещений с повторениями обозначают
. Соответственно число сочетаний и размещений с повторениями обозначают 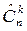 и
и 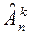 . В том случае, когда мощность выборочного множества совпадает с размером выборки (n=k), размещения называют перестановками на множестве из n элементов. Число таких перестановок обозначается Pn. Сейчас мы выведем формулы для вычисления всех этих величин.
. В том случае, когда мощность выборочного множества совпадает с размером выборки (n=k), размещения называют перестановками на множестве из n элементов. Число таких перестановок обозначается Pn. Сейчас мы выведем формулы для вычисления всех этих величин.
 2015-01-30
2015-01-30 2394
2394







