1. Плотность тока в никелиновом проводнике длиной 25 м равна
1 МА/м2. Определить напряжение на концах проводника.
Дано: l = 25 м; j = 106 А/м2; ρ = 4 · 10-7 Ом · м.
Найти: U
Решение. По закону Ома, в дифференциальной форме плотность тока j в проводнике пропорциональна напряженности Е поля в проводнике 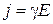 ,
,
где 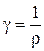 — удельная проводимость.
— удельная проводимость.
С другой стороны, 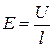 , где U — напряжение на концах проводника длиной l. Тогда
, где U — напряжение на концах проводника длиной l. Тогда 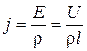 , откуда
, откуда 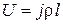 ; Подставим численные значения:
; Подставим численные значения:
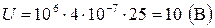 .
.
2. Напряжение на концах проводника сопротивлением 5 Ом за 0,5 с равномерно возрастает от 0 до 20 В. Какой заряд проходит через проводник за это время?
Дано: R = 5 Ом; t = 0,5 с; U 1 = 0; U 2= 20 В.
Найти: q
Решение. За время dt по проводнику переносится заряд 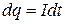 ,
,
где 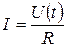 — ток в проводнике, R — сопротивление проводника; U (t) —напряжение на концах проводника.
— ток в проводнике, R — сопротивление проводника; U (t) —напряжение на концах проводника.
Напряжение U линейно изменяется со временем, т. е, можно записать 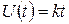 , где
, где 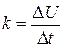 — коэффициент пропорциональности,
— коэффициент пропорциональности,
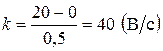 .
.
Заряд q, перенесённый по проводнику за 0,5 с, будет
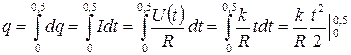 ;
;
Подставим числовые данные: 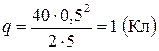 .
.
3. Температура вольфрамовой нити электролампы 2000 °С, диаметр 0,02 мм, сила тока в ней 4 А. Определить напряженность поля в нити.
Дано: t = 2000 °С; d = 2 · 10-5 м; I = 4 А; ρ0 = 5,5 · 10-8 Ом · м;
α = 5,2 · 10-3 К-1 (определено по справочнику).
Найти: Е.
Решение. По определению, плотность тока 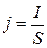 , где I - сила тока, S – площадь поперечного сечения нити, определяемое по формуле:
, где I - сила тока, S – площадь поперечного сечения нити, определяемое по формуле: 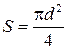 .
.
По закону Ома, в дифференциальной форме плотность тока
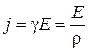 , где Е — напряжённость поля в нити, ρ — удельное сопротивление,
, где Е — напряжённость поля в нити, ρ — удельное сопротивление, 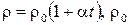 — удельное сопротивление вольфрама при t = 0 °С, α - температурный коэффициент сопротивления. Из уравнения
— удельное сопротивление вольфрама при t = 0 °С, α - температурный коэффициент сопротивления. Из уравнения
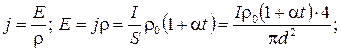
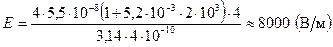 .
.
4. Внутреннее сопротивление аккумулятора 1 Ом. При силе тока 2 А КПД электрической цепи равен 0,8. Определить ЭДС аккумулятора.
Дано: r = 1 Ом; I = 2 А; η = 0,8.
Найти: ε.
Решение. КПД определяется по формуле 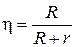 .
.
Отсюда 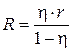 . Запишем закон Ома для замкнутой цепи
. Запишем закон Ома для замкнутой цепи 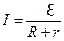 .
.
Выражая э.д.с. ε, получим: 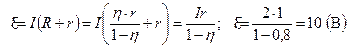 .
.
5. Определить ЭДС электрической цепи, содержащей аккумуляторную батарею, ток короткого замыкания которой 10 А. При подключении к аккумуляторной батарее резистора сопротивлением 9 Ом сила тока в цепи равна 1 А.
Дано: I кз = 10 A; R = 9 Ом; I = 1 А.
Найти: ε.
Решение. По закону Ома для замкнутой цепи: 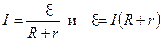 .
.
При коротком замыкании цепи внешнее сопротивление R = 0 и 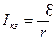 , откуда
, откуда 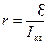 . Тогда
. Тогда 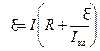 или
или 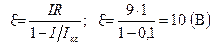 .
.
6. К источнику тока подключают один раз резистор сопротивлением 1 Ом, другой раз — 4 Ом. В обоих случаях на резисторах за одно и то же время выделяется одинаковое количество теплоты. Определить внутреннее сопротивление источника тока.
Дано: R 1= 1 Ом; R 2= 4 Ом; t 1 = t 2 = t, Q l = Q 2.
Найти: r.
Решение. По закону Ома, 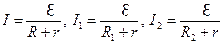 .
.
По закону Джоуля – Ленца, количество теплоты Q, выделяемое в проводнике при прохождении тока за время t, равно: 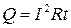 .
.
Так как 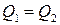 , то
, то 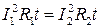 , тогда
, тогда 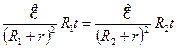 ;
;
После математических преобразований получим: 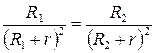 ;
;
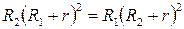 ;
; 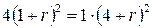 ;
; 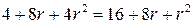 ;
;
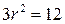 ;
; 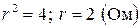 .
.
7. Сила тока в резисторе линейно возрастает за 4 с от 0 до 8 А. Сопротивление резистора 10 Ом. Определить количество теплоты, выделившееся в резисторе за первые 3 с.
Дано: t 0 = 0; t 1= 4 с; I = 0; 1 1 = 8 A; t 2= 3 с; R = 10 Ом.
Найти: Q.
Решение. По закону Джоуля - Ленца
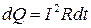 .
.
Так как сила тока является функцией времени, то
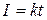 ,
,
где k — коэффициент пропорциональности, численно равный приращению тока в единицу времени: 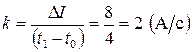 .
.
Следовательно, 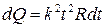 .
.
За первые 3 с выделится количество теплоты, равное
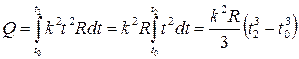 .
.
Подставляя числовые значения, получим
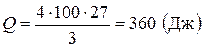 .
.
8. Батарея состоит из пяти последовательно соединенных элементов. ЭДС каждого 1,4 В, внутреннее сопротивление 0,3 Ом. При каком токе полезная мощность батареи равна 8 Вт? Определить наибольшую полезную мощность батареи.
Дано: εi = 1,4 В; ri = 0,3 Ом; Р п = 8 Вт; п = 5.
Найти: I, Р п mах.
Решение. Полезная мощность батареи 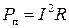 . (1)
. (1)
Сила тока определяется по закону Ома: 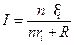 . (2)
. (2)
Здесь 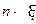 — ЭДС, а
— ЭДС, а 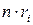 — внутреннее сопротивление п последовательно соединенных элементов.
— внутреннее сопротивление п последовательно соединенных элементов.
Выразим R из (1): 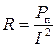 и, подставив это выражение в (2), получим
и, подставив это выражение в (2), получим
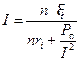 (3)
(3)
или 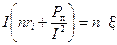 . (4)
. (4)
Преобразуя выражение (4), получим квадратное уравнение относительно I:
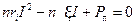 .
.
Решая квадратное уравнение, найдем: 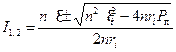 .
.
Подставляя числовые значения, получим:
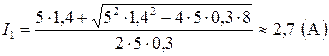 ;
;
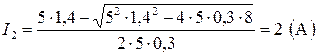 .
.
Для того чтобы определить наибольшую полезную мощность батареи, найдем зависимость её от внешнего сопротивления. Подставим в уравнение (1) выражение (2): 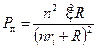 . (5)
. (5)
Из этой формулы следует, что при постоянных величинах εi и ri мощность является функцией одной переменной — внешнего сопротивления R. Известно, что эта функция имеет максимум, если 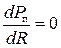 , следовательно, имеем:
, следовательно, имеем:
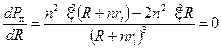 ,
,
или 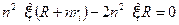 . (6)
. (6)
Таким образом, задача сводится к отысканию сопротивления внешней цепи. Из решения уравнения (6) следует, что 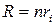 .Подставляя найденное значение R в формулу (5), имеем:
.Подставляя найденное значение R в формулу (5), имеем: 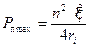 .
.
Производя вычисления, найдем 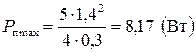 .
.
 2015-01-07
2015-01-07 12360
12360
