Задание 6.11

На основании данных задания 6.1 определите общую тенденцию ряда методами:

· Увеличения интервалов;

· Определения средней скользящей;

· Аналитического выравнивания.

На основании аналитического выравнивания сделайте точечный и интервальный прогноз на 2 года.

Для расчетов используйте таблицу 6.5.

Таблица 6.5

Выявление основной тенденции численности мужчин Вологодской области

Годы	Численность мужчин на 1 янв., тыс.чел. yi	В среднем за 2 года	Средняя скользящая по 3-хлетиям	Условное обозначение времени	Выравненные уровни ряда	-yi	-yi)2
t	t2	yit
Итого

Задание 6.12

Имеются данные о численности безработных в РФ по материалам выборочных обследований населения по проблемам занятости (по методологии МОТ). Рассчитайте отсутствующие в таблице сведения и занесите их в таблицу.

Таблица 6.6

Численность безработных в РФ

Годы	Численность безработных, тыс. человек	Изменение по сравнению с предыдущим годом
абсолютный прирост, руб	темп роста, %	темпы прироста, %	абсолютное значение 1% прироста, тыс.чел.
		-51
			86,4
				4,4
		-728			63,73

Тема 7: Экономические индексы

Индексом в статистике называется относительный показатель, характеризующий изменение величины какого-либо явления во времени, в пространстве или в сравнении с эталоном.

В зависимости от объекта, подлежащего изучению индексным методам (сложная совокупность или её элементы), индексы подразделяются соответственно на общие и индивидуальные.

Индивидуальные индексы — характеризуют изменение отдельных единиц (элементов) изучаемой сложной совокупности.

В экономических расчетах чаще всего используются общие индексы. В зависимости от цели исследования и наличия исходных данных используют различные формы построения общих индексов — агрегатную или среднюю (среднюю из индивидуальных индексов).

Числитель и знаменатель агрегатного индекса представляют собой сумму произведений двух величин, одна из которых меняется (индексируемая величина) – это признак, изменение которого изучается, а другая выступает соизмерителем и остается неизменной в числителе и знаменателе (вес) индекса.

Например, агрегатный индекс объема:

Агрегатный индекс цены:

Средний арифметический индекс - чаще всего применяется на практике для расчета сводных индексов количественных показателей:

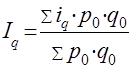
Средний гармонический индекс - применяется чаще для качественных показателей

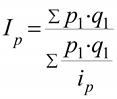
Индексы средних уровней

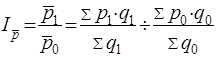Изменение среднего уровня качественного показателя оценивается с помощью индекса переменного состава. Так, например, индекс средней цены равен:

На формирование среднего уровня качественного показателя (цены, себестоимости, трудоемкости) оказывают влияние 2 фактора (2 субиндекса):

Индекс постоянного состава показывает, как изменяется средний уровень показателя в результате изменения его индивидуальных значений при неизменной структуре. Например, индекс средней цены постоянного состава:

=

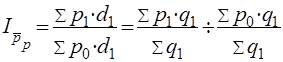
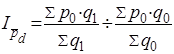Индекс структурных сдвигов позволяет оценить влияние изменения структуры совокупности на средний показатель:

=

Перечисленные индексы образуют систему:

Студент должен

знать:

· сущность индексного метода;

· определение и классификацию индексов;

· принципы их построения;

· взаимосвязи индексов

уметь:

· выделять в агрегатном индексе индексируемую величину и вес;

· строить индексы;

· определять тенденции изменения исследуемых явлений во времени и в пространстве с помощью различных индексов