Решение задачи линейного программирования симплексным методом

Рассмотрим, как, исходя из начального опорного плана задачи линейного программирования, с помощью симплексного метода найти оптимальный план.

Продолжим рассмотрение задачи (2.1)-(2.3), опорный план которой 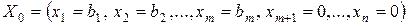. Для исследования данного плана на оптимальность (по условию оптимальности плана задачи линейного программирования) необходимо векторы 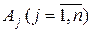системы ограничений (2.2) разложить по базисными векторами 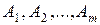и рассчитать значение оценок .

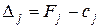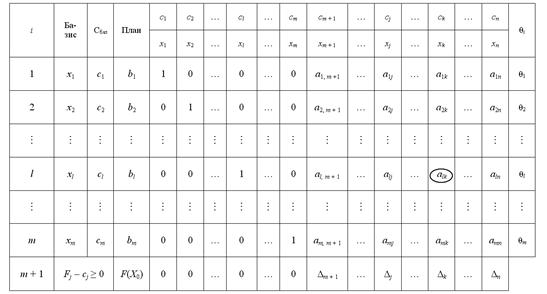
Все дальнейшие вычисления удобно проводить в симплексной таблице (табл.2.1).

В столбце «Базис» записанные переменные, которые отвечают базисным векторам, а в столбце «С_баз» – коэффициенты функционала соответствующих базисных векторов. В столбце «План» – начальный опорный план 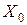, в этом же столбце в результате вычислений получают оптимальный план. В столбцах 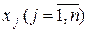записанные коэффициенты разложения каждого j- го вектора по базисным векторам, которые отвечают в первой симплексной таблице коэффициентам при переменных в системе (4.2). В (m+1)-ой строке в столбце «План» записывают значение функционала для начального опорного плана 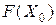, а в других столбцах 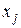– значение оценок 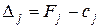. Эта строка симплексной таблицы называют оценочной.

Значения 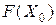находят подстановкой компонент опорного плана в целевую функцию, а значение 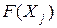– при подстановке коэффициентов разложения каждого j- го вектора по векторам базиса, т.е. эти значения в табл.2.1 получают как скалярное произведение:

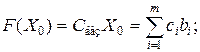
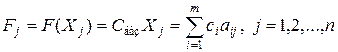где сi – коэффициенты функционала, которые отвечают векторам базиса.

Таблица 2.1 - Первая симплексная таблица для решения задач линейного программирования

После заполнения табл.2.1 рассчитывают значение оценок плана (последняя строка): 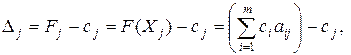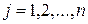. Потом согласно условию оптимальности плана задачи линейного программирования, если все 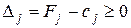(для задачи на максимум), то план является оптимальным. Допустим, что одна из оценок 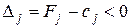, тогда план 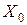не является оптимальным и необходимо осуществить переход к следующему опорному плану, которому будет соответствовать большему значению функционала. Если отрицательных оценок несколько, то включению в базис подлежит вектор, который выбирается как 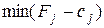. Минимум находят для тех индексов j, где 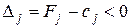. Если существует несколько одинаковых значений оценок, которые отвечают 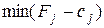, то из соответствующих им векторов к базису включают тот, которому отвечает максимальное значение функционала.

Если хотя бы для одной отрицательной оценки 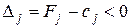все коэффициенты разложения 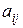соответствующего вектора отрицательные, то это означает, что функционал является неограниченным на многограннике решений, т.е. многогранник в данном виде представляет собой неограниченную область и решением задачи есть .

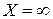Пусть 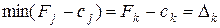, т.е. минимальное значение достигается для k- го вектора 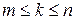. Тогда к базису включается вектор 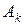. Соответствующий столбик симплексной таблицы называют направляющим.

Для того, чтобы выбрать вектор, который необходимо вывести из базиса (согласно процедуре перехода от одного опорного плана задачи к другому – п.4.2), рассчитывают последний столбик табл.2.1 – значение .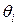

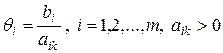Из рассчитанных значений необходимо выбрать меньше всего 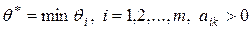. Тогда из базиса исключают i - ий вектор, которому отвечает .

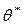Допустим, что 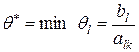отвечает вектору, который находится в l- му строке табл.2.1. Соответствующая строка симплексной таблицы называют направляющим.

Пересечением направляющего столбика и направляющей строки определяется элемент симплексной таблицы a_lk, который называют разрешающим элементом. С помощью элемента a_lk и метода Жордана-Гаусса рассчитывают новую симплексную таблицу, которая будет определять следующий опорный план задачи.

Для определения нового опорного плана необходимо все векторы разложить по векторам нового базиса. Вектор А_k, который необходимо вводить в базис, в представлении по начальныму базису имеет вид:

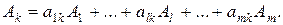(2.16)

Вектор А_l выходит из базиса, и его Разложение по новому базису получим из выражения (2.16):

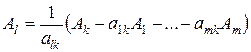. (2.17)

Разложение вектора А₀ по начальному базису имеет вид:

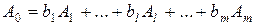. (2.18)

Для записи разложения вектора в новом базисе подставим выражение (2.17) в уравнение (2.18), имеем:

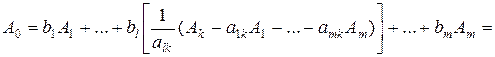
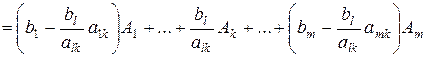Итак, значение компонент следующего опорного плана рассчитываются по формулам:

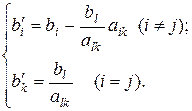(2.19)

Разложение по начальному базису любого из векторов имеет вид:

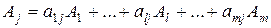. (2.20)

Разложение по новому базису получим подстановкой (2.17)
в (2.20):

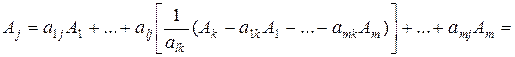
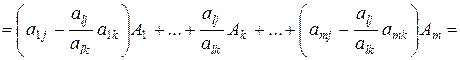
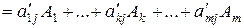Новый план: 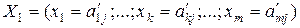, где

(2.21)

Формулы (2.19) и (2.21) являются формулами полных исключений Жордана-Гаусса.

Итак, чтобы получить коэффициенты разложения векторов 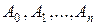по векторам нового базиса (переход к следующему опорному плану и созданию новой симплексной табл.2.2), необходимо:

1) разделить все элементы направляющей строки на разрешающий элемент;

2) рассчитать все другие элементы по формулам полных исключений Жордана-Гаусса (правило прямоугольника).

Потом необходимо осуществить проверку новых значений оценочной строки. Если все F_j – с _j ³ 0, то план Х₁ — оптимальный, иначе переходят к отысканию следующего опорного плана. Процесс продолжают до получения оптимального плана, или установления факта отсутствия решения задачи.

Если в оценочной строке последней симплексной таблицы оценка F_j – с _j ³ 0 отвечает свободной (небазисной) переменной, то это означает, что задача линейного программирования имеет альтернативный оптимальный план. Получить его можно, выбирая разрешающий элемент в указанном столбике таблицы и осуществив один шаг (одну итерацию) симплекс-методом. В результате получим новый опорный план, которому отвечает то самое значение функционала, которое и для предыдущего плана, т.е. функционал достигает максимального значения в двух точках многогранника решений, а итак, по свойству решений задачи линейного программирования такая задача имеет бесконечное множество оптимальных планов.

Решение задачи линейного программирования на отыскание минимального значения функционала отличается лишь условием оптимальности опорного плана. К базису включают вектор, для которого 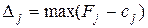, где максимум находят для тех j, которым отвечают 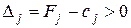. Все другие процедуры симплексного метода осуществляются аналогично, как в задаче линейного программирования на отыскание максимального значения функционала.