Регрессионные модели и способы их расчета

Пусть в результате измерений в процессе опыта получена таблица некоторой зависимости f(x):

			…		…
			…		…

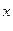
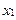
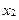
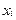
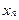
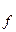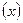
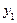
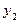
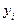
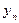
Нужно найти формулу, выражающую эту зависимость аналитически.

Поставим задачу так, чтобы с самого начала учитывался характер исходной функции. Найти функцию заданного вида 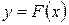, которая в узловых точках принимает как можно более близкие значения к значениям из таблицы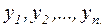

Практически вид приближающей функции F устанавливают следующим образом: по таблице строится точечный график функции f, а затем проводится плавная кривая, по возможности наилучшим образом отражающая характер расположения точек:

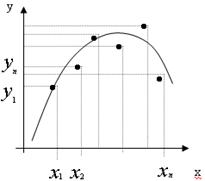
В узловых точках функции f(x) и F(x) будут отличаться на величину 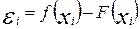. (1) Отклонения 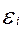могут принимать «+» или «-» значения. Чтобы эти знаки не учитывать, возведем каждое отклонение в квадрат и просуммируем квадраты отклонений по всем узлам:

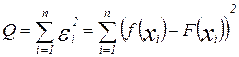. (2)

Метод построения приближающих функции F(x) из условия минимума величины Q называется методом наименьших квадратов.

В качестве приближающих функций в зависимости от характера точечного графика функции f часто используют следующие функции:

1. 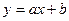;	3. 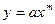;	5. 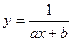;	7. ;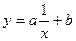
2. 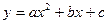;	4. 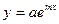;	6. 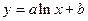;	8. .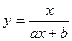

Здесь 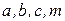– параметры. Когда вид приближающей функции (1-8) установлен, задача сводится только к отысканию параметров.

Рассмотрим метод их нахождения в общем виде на примере F с тремя параметрами:

Пусть 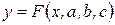(3), где 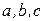- постоянные, 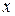- независимая переменная, тогда значения 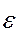и 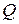из выражения (2) примет вид

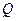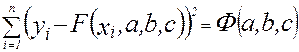= (4)

и является функцией трех переменных (параметров a, b, c). Задача сводится к отысканию ее минимума.

Используем необходимое условие экстремума частная производная функции должна быть равна нулю: 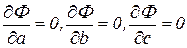, т. е. получаем систему из следующих уравнений

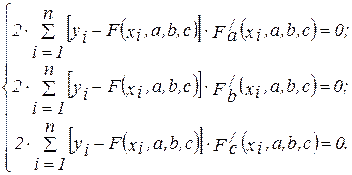(5)

Решив эту систему трех уравнений с тремя неизвестными относительно параметров a, b, c, мы и получим конкретный вид искомой функции F(x, a, b, c).

Изменение количества параметров не изменит самого подхода, а приведет лишь к изменению количества уравнений в системе (5).

Построив функцию F(x), находят сумму квадратов отклонений Q. Из двух различных приближений выбирают то, для которого эта сумма минимальна. Обычно при обработке экспериментальных данных, определенных с погрешностью e, согласуют погрешность e с погрешностью МНК, т. е. 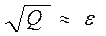. Это дает оптимальный результат.