2015-01-07
1433
Уравнение линии степенной функции иногда еще называют геометрической регрессией. Покажем, что нахождение приближенных функций с двумя параметрами F(x, a, b) в виде элементарных функций может быть сведено к нахождению параметров линейной функции.
Будем искать функцию в виде: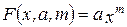 
(1)
Предположим, что любые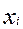 
> 0 и 
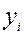> 0.
Прологарифмируем (1):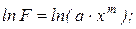 
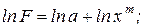
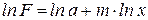(2).
Т. к.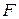 
– приближающая функция для f, то 
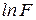– приближающая для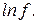 
Введем новую переменную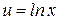 
и обозначим 
(*)
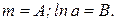Тогда 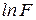- функция от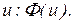 
Тогда (2) примет вид: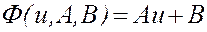 
(3),
т. е. задача свелась к отысканию приближающей функции в виде линейной.
Практически при нахождении приближающей степенной функции необходимо выполнить следующие действия:
· По исходной таблице составить новую, прологарифмировав значения х и у.
· По новой таблице найти параметры А и В для линейной функции вида (3).
· Используя введенные обозначения (*), найти а и m и подставить в выражение (1).
