Цель работы:
1. Ознакомить студентов с методами измерения поверхностного натяжения жидкостей.
2. Изучить зависимость коэфициента поверхностного наяжения от концентрации раствора и температуры.
3. Изучить адсорбцию поверхностно-активных веществ (ПАВ) на поверхности жидкости.
Существует большой класс физических, химических, биологических и природных явлений, ход и течение которых существенно определяется особым энергетическим состоянием поверхности раздела фаз. Это – явления смачивания, растекания, диспергирования, эмульгирования, адсорбции и др.
|
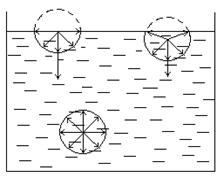 Особые свойства поверхностного слоя жидкости объясняются тем, что число ближайших соседей молекул этого слоя отличается от их числа внутри объёма жидкости. В тонком слое на границе жидкости с паром число соседей меньше, чем в объёме. В результате силы, действующие на каждую молекулу в поверхностном слое, оказываются неуравновешеными: равнодействующая этих сил направлена в сторону жидкости перпендикулярно её поверхности. Вследствии этого поверхностный слой производит на остальную жидкость давление. Это так называемое внутренне давление, учитываемое в уравнении Ван-дер-Ваальса (
Особые свойства поверхностного слоя жидкости объясняются тем, что число ближайших соседей молекул этого слоя отличается от их числа внутри объёма жидкости. В тонком слое на границе жидкости с паром число соседей меньше, чем в объёме. В результате силы, действующие на каждую молекулу в поверхностном слое, оказываются неуравновешеными: равнодействующая этих сил направлена в сторону жидкости перпендикулярно её поверхности. Вследствии этого поверхностный слой производит на остальную жидкость давление. Это так называемое внутренне давление, учитываемое в уравнении Ван-дер-Ваальса (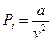 ). Численное значение внутреннего давления громадно. Для воды, например,оно равно
). Численное значение внутреннего давления громадно. Для воды, например,оно равно 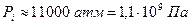 . Взаимное притяжение между молекулами жидкости вызывает не только добавочное молекулярное давление, но и силу, направленную вдоль поверхности и стремящуюся ее сократить. Поскольку из всех возможных состояний наиболее устойчивым является то, в котором энергия системы минимальна, то всякая жидкость, чтобы удовлетворить этому условию, всегда стремится уменьшить свою поверхность. Если на поверхности жидкости мысленно провести произвольную линию, то нормально к ней по касательной к поверхности в противоположные стороны будут действовать силы поверхностного натяжения. Эти противоположно направленные силы уравновешивают друг друга. Поэтому для характеристики поверхностного натяжения определенной жидкости необходимо определить силу натяжения, отнесенную к единице длины произвольной линии, проведенной на поверхности.
. Взаимное притяжение между молекулами жидкости вызывает не только добавочное молекулярное давление, но и силу, направленную вдоль поверхности и стремящуюся ее сократить. Поскольку из всех возможных состояний наиболее устойчивым является то, в котором энергия системы минимальна, то всякая жидкость, чтобы удовлетворить этому условию, всегда стремится уменьшить свою поверхность. Если на поверхности жидкости мысленно провести произвольную линию, то нормально к ней по касательной к поверхности в противоположные стороны будут действовать силы поверхностного натяжения. Эти противоположно направленные силы уравновешивают друг друга. Поэтому для характеристики поверхностного натяжения определенной жидкости необходимо определить силу натяжения, отнесенную к единице длины произвольной линии, проведенной на поверхности. Коэффициент поверхностного натяжения 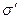 можно определить как отношение сил поверхностного натяжения к длине контура
можно определить как отношение сил поверхностного натяжения к длине контура 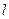 , ограничивающего поверхность
, ограничивающего поверхность 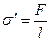 . В системе СИ
. В системе СИ 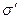 имеет размерность
имеет размерность 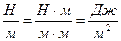 . Поскольку
. Поскольку 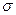 и
и 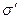 определяют один и тот же эффект, а их размерности одинаковы, то
определяют один и тот же эффект, а их размерности одинаковы, то 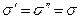 . С другой стороны можно сказать, что силы внутреннего давления обуславливают самопроизвольное сокращение поверхности жидкости. При этом они совершают работу
. С другой стороны можно сказать, что силы внутреннего давления обуславливают самопроизвольное сокращение поверхности жидкости. При этом они совершают работу 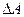 . С точки зрения термодинамики это эквивалентно наличию в поверхностном слое свободной поверхностной энергии
. С точки зрения термодинамики это эквивалентно наличию в поверхностном слое свободной поверхностной энергии 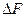 , которая определяется работой, затрачиваемой для увеличения площади поверхности жидкости (
, которая определяется работой, затрачиваемой для увеличения площади поверхности жидкости (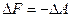 ). Работа, необходимая для изотермического увеличения поверхности на единицу площади называется удельной свободной поверхносьной энергией
). Работа, необходимая для изотермического увеличения поверхности на единицу площади называется удельной свободной поверхносьной энергией 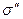 . В системе СИ размерность
. В системе СИ размерность 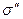
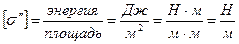 .
.
Следовательно, поверхностным натяжением называют силу, действующую на единицу длины контура, или свободную энергию, приходящуюся на единицу площади поверхности. Оба эти определения эквивалентны. Размерности 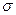 в обоих случаях одинаковы.
в обоих случаях одинаковы.
Наличие поверхностного натяжения приводит к появлению дополнительного давления, действующего на искривленную поверхность жидкости. Зависимость этого давленя от кривизны поверхности и межфазного поверхностного натяжения установил Лаплас
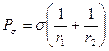 ,
,
где 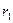 и
и 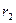 – главные радиусы кривизны в выбранной точке поверхности жидкости. Для шарообразной капли
– главные радиусы кривизны в выбранной точке поверхности жидкости. Для шарообразной капли 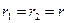 и, следовательно,
и, следовательно, 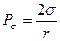 . Добавочное молекулярное давление всегда направлено к центру кривизны. Поэтому для выпуклой поверхности оно направлено внутрь жидкости, для вогнутой – наружу.
. Добавочное молекулярное давление всегда направлено к центру кривизны. Поэтому для выпуклой поверхности оно направлено внутрь жидкости, для вогнутой – наружу.
Капиллярные явления.
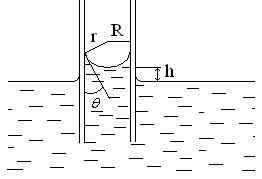
Форма поверхности жидкости определяется взаимодействием ее с ограничивающими твердыми телами. Условия равновесия на линии раздела жидкость-газ-твердая стенка удобно рассмотреть в узких трубках, диаметр которых измеряется долями миллиметра. Такие трубки называют капиллярами. Если жидкость смачивает стенку, то она у края поднимается, образуя вогнутый мениск. В широком сосуде мениск, захватывающий лишь небольшую часть поверхности, непосредственно прилегающую к стенкам, не оказывает существенного влияния на давление жидкости. В тонких же капиллярных трубках мениск захватывает всю поверхность жидкости, искривляет ее и, следовательно, может оказывать значительное дополнительное давление на жидкость. Поэтому, если один конец узкой трубки опустить в сосуд со смачивающей ее стенки жидкостью, то последня поднимается у стенки и образует вогнутую поверхность, близкую к шаровой. Давление внутри трубки становится меньшим, чем в окружающей жидкости, на величину 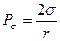 . За счет разности этих давлений жидкость в трубке поднимается до такой высоты
. За счет разности этих давлений жидкость в трубке поднимается до такой высоты 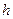 , чтобы и
, чтобы и 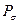 уравновесилось избытком гидростатического давления
уравновесилось избытком гидростатического давления 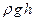 :
:
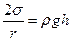 .
.
|
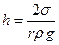 . Выразив радиус кривизны
. Выразив радиус кривизны 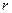 через краевой угол
через краевой угол 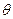 и радиус трубки
и радиус трубки 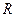 (
(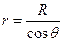 ), получим, что
), получим, что
|
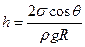 . (1)
. (1) Если капиллярную трубку опустить одним концом в жидкость, не смачивающую ее стенок, то образуется выпуклый мениск и уровень жидкости внутри трубки будет ниже, чем в широком сосуде. Имеет место опускание жидкости в трубке. Последнюю формулу можно использовать для определения 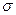 по измерениям высот поднятия жидкости в капиллярных трубках разных радиусов.
по измерениям высот поднятия жидкости в капиллярных трубках разных радиусов.
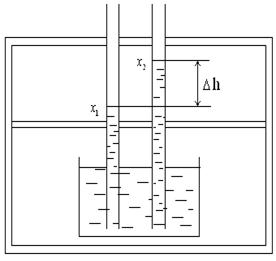
Если использовать два капилляра с радиусами 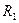 и
и 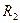 , то можно проградуировать прибор (см. рис.) по жидкости с известным
, то можно проградуировать прибор (см. рис.) по жидкости с известным 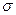 , например, по воде. Оба капилляра, тщательно промытые, опущены в чашечку с водой. Перемещая тубус микроскопа вдоль вертикальной шкалы с нониусом, совмещают горизонтальную нить пререкрестия с касательной к мениску жидкости сначала в одной, а потом в другой трубке. При этом записывают отсчеты по вертикальной шкале. Пусть
, например, по воде. Оба капилляра, тщательно промытые, опущены в чашечку с водой. Перемещая тубус микроскопа вдоль вертикальной шкалы с нониусом, совмещают горизонтальную нить пререкрестия с касательной к мениску жидкости сначала в одной, а потом в другой трубке. При этом записывают отсчеты по вертикальной шкале. Пусть 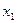 и
и 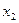 – отсчеты, соответствующие положениям менисков воды в трубке. Тогда, очевидно,
– отсчеты, соответствующие положениям менисков воды в трубке. Тогда, очевидно, 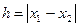 будет разностью высот подъема жидкости в них:
будет разностью высот подъема жидкости в них: 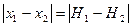 . Используя (1) для воды с коэффициентом поверхностного натяжения
. Используя (1) для воды с коэффициентом поверхностного натяжения 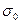 и плотностью
и плотностью 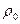 , получим для разности высот ее поднятия в каппилярах с радиусами
, получим для разности высот ее поднятия в каппилярах с радиусами 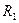 и
и 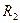
 выражение
выражение
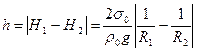 . (2)
. (2)
Если в аналогичных измерениях, проведенных с исследуемой жидкостью, получены отсчеты 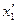 и
и 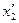 соответственно, то для разности высот ее поднятия в тех же капиллярах, получим
соответственно, то для разности высот ее поднятия в тех же капиллярах, получим
|
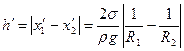 , (3)
, (3) где 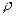 – плотность исследуемой жидкости при температуре опыта,
– плотность исследуемой жидкости при температуре опыта, 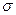 – значение поверхностного натяжения.
– значение поверхностного натяжения.
Разделив выражения (2) и (3) друг на друга, получим рабочую формулу для расчета коэффициента 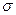 :
:
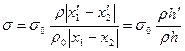 . (4)
. (4)
Метод максимального давления воздуха в пузырьке.
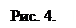 |
 Исследования температурной и концентрационной зависимости поверхностного натяжения жидкостей удобнее проводить методом максимального давления в пузырьке, предложенном П.А.Ребиндером. Реализующий этот метод прибор состоит из наполненного водой аспиратора А, соединенного с манометром М и закрытым сосудом В, в который налита исследуемая жидкость. Эти элементы соединены друг с другом посредством четырехколенной трубки с отростком D с краном, обеспечивающем возможность соединения системы с атмосферой. Сосуд В помещают в стакан с водой и приспособлением для подогрева. Через отверстие в пробке в сосуд В введена стеклянная трубка, конец которой стянут в тонкий капилляр К – "кончик". Кончик помещается на уровне жидкости так, чтобы он только соприкасался с ее поверхностью; другой конец трубки открытый. Если закрыть кран Д и открыть кран аспиратора, то из него ночнёт вытекать вода. Это приведет к понижению давления в аспираторе и в сосуде В. Уменьшение давления будет сопровождаться возрастанием разности уровней жидкости в манометре. Под действием атмосферного давления Pатм в исследуюмую жидкость при некотором максимальном разрежении PВ в сосуде В через кончик порываеься пузырёк воздуха. вэтот момент разность атмосферного давления и давления воздуха в сосуде В Pатм - PВ, измеряемая манометром М, уравновешивает давление P, создаваемое поверхностным натяжением жидкости, стремящимся раздавить образующийся пузырёк. Так как кончик расположен на уровне жидкости, то все гидростатические поправки к давлению
Исследования температурной и концентрационной зависимости поверхностного натяжения жидкостей удобнее проводить методом максимального давления в пузырьке, предложенном П.А.Ребиндером. Реализующий этот метод прибор состоит из наполненного водой аспиратора А, соединенного с манометром М и закрытым сосудом В, в который налита исследуемая жидкость. Эти элементы соединены друг с другом посредством четырехколенной трубки с отростком D с краном, обеспечивающем возможность соединения системы с атмосферой. Сосуд В помещают в стакан с водой и приспособлением для подогрева. Через отверстие в пробке в сосуд В введена стеклянная трубка, конец которой стянут в тонкий капилляр К – "кончик". Кончик помещается на уровне жидкости так, чтобы он только соприкасался с ее поверхностью; другой конец трубки открытый. Если закрыть кран Д и открыть кран аспиратора, то из него ночнёт вытекать вода. Это приведет к понижению давления в аспираторе и в сосуде В. Уменьшение давления будет сопровождаться возрастанием разности уровней жидкости в манометре. Под действием атмосферного давления Pатм в исследуюмую жидкость при некотором максимальном разрежении PВ в сосуде В через кончик порываеься пузырёк воздуха. вэтот момент разность атмосферного давления и давления воздуха в сосуде В Pатм - PВ, измеряемая манометром М, уравновешивает давление P, создаваемое поверхностным натяжением жидкости, стремящимся раздавить образующийся пузырёк. Так как кончик расположен на уровне жидкости, то все гидростатические поправки к давлению 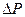 могут быть исключены из равенства
могут быть исключены из равенства 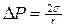 следует формула для поверхностного натяжения σ:
следует формула для поверхностного натяжения σ: 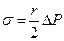
Неизвестный (минимальный) радиус кривизны возникающего пузырька r нет необходимости определять при использовании относительного метода. Сначала поводят измерения P0 для воды, поверхностное натяжение которой σ0 известно. Затем определяют постоянную прибора 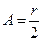 ;
; 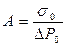 .
.
Поверхностное натяжение исследуемой жидкости определяется в относительном методе по формуле
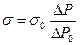 ,
,
где 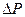 разность уровней h1 и h2 в манометрических трубках.
разность уровней h1 и h2 в манометрических трубках.
В этой лабораторной работе выполняется три задачи. Эксперименты и вычисления выполняются в следующем порядке.
Задача №1. определение коэффициента поверхностного натяжения жидкости методом капилярных трубок.
1. Полученные у лаборанта 2 капилляра тщательно промыть и опустить в чашечку с дистиллированной водой.
2. Наблюдая в микроскоп манометра, добиться резкого изображения мениска в одной из трубок. Наблюдаемое изображение будет перевернутым.
3. Перемещая тубус микроскопа по вертикальной шкале катетометра, совместить горизонтальную нить перекрестия с касательной к мениску в одной трубке и сделать отсчет 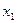 . Затем совместить нить с мениском в другой трубке и сделать отсчет
. Затем совместить нить с мениском в другой трубке и сделать отсчет 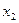 .
.
4. Подвигать столбцы жидкости в трубках, слегка приподняв и опустив их на прежнее место, вновь сделать отсчеты 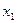 и
и 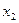 . Операцию отсчета
. Операцию отсчета 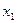 и
и 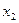 повторить три раза.
повторить три раза.
5. Промыть капилляры исследуемым расствором спирта и опустить в чашечку с этим раствором.
6. Проделать такие же измерения с этим растворм три раза.
7. Результаты отсчетов, определения разности уровней h, их средних значений и погрешностей последних, а также табличные данные о 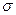 и
и 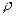 воды и раствора при температуре опыта записать в таблицу.
воды и раствора при температуре опыта записать в таблицу.
| № | Вода | Раствор спирта C=___% | ||||
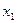 | 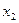 | 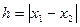 | 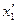 | 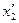 | 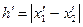 | |
Среднее 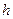 | Среднее 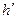 |
8. Расчет поверхностного натяжения поводить по формуле (4). Расчет погрешности 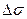 проводить по формуле
проводить по формуле
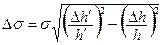 ;
;
пренебрегая погрешностями табличных данных 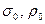 и
и 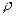 .
.
Задача №2. Изучение зависимости поверхностного натяжения водного раствора спирта от концентрации методом максимальноо давелния в пузырьке.
1. Ополоснув сосуд В и кончик трубки прибора Ребиндера водой, наливают в него воду и опускают кончик в воду так, чтобы он только касался её поверхности. Для проверки установки, открыв кран Д, соединяют систему с атмосферой. Если манометр устанавливается на нуле, то система трубок не засорена.
2. Закрыв кран Д, создают разность давлений в системе путём открытия крана аспиратора А. если показания манометра изменяются, то в системе есть течь, коорую необходимо устранить.
3. Добиваются медленного регулярного отрыва пузырьков, чтобы изменение давления происходило достаточно медленно и можно было бы легко отсчитывать высоты уровней в манометре в момент отрыва пузырька.
4. Определяют разность давлений 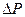 для 10-ти пузырьков, рассчитывают среднее значение и порешность ее измерения.
для 10-ти пузырьков, рассчитывают среднее значение и порешность ее измерения.
5. Закрыв кран аспиратора, открывают кран Д, осторожно выливают воду из сосуда В и заливают в него исследуемые растворы, в порядке возрастания концетрации. Для каждого из растворов определяют среднее значение 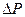 из 10 измерений и погрешность.
из 10 измерений и погрешность.
6. Результаты измерений, расчетов 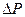 и их средних значений и погрешностей, температуру опыта и табличные значения
и их средних значений и погрешностей, температуру опыта и табличные значения 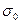 при этой температуре заносят в таблицу.
при этой температуре заносят в таблицу.
| Жидкость | Максимальное давление 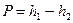 мм. рт. ст. мм. рт. ст. | Поверхностное натяжение 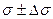 (Дж/м2) (Дж/м2) | ||||||||||
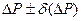 | ||||||||||||
| Вода 0% | ||||||||||||
| 10% | ||||||||||||
| 15% | ||||||||||||
| 20% |
Расчет поверхностного натяжения проводить по формуле (5). Расчет погрешностей 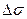 поводить по формуле
поводить по формуле
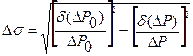
7. По данным первого и последнего столбцов таблици строят график зависимости поверхностного натяжения водного раствора спирта от концентрации C.
Задача №3. Изучение зависимости поверхностного натяжения жидкости от температуры.
1. Для одного из растворов спирта (по указанию преподавателя) провести измерения максимального давления 10-ти пузырьковпри нескольких установившихся температурах(30°С, 40°С, 50°С) воды в подогреваемом стакане.
2. Для каждой из температур провести расчет среднего значения 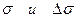 . Результаты измерений и расчетов занести в таблицу.
. Результаты измерений и расчетов занести в таблицу.
| Темпера-тура, °С | Максимальное давление 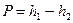 мм. рт. ст. мм. рт. ст. | Поверхностное натяжение 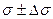 (Дж/м2) (Дж/м2) | ||||||||||
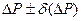 | ||||||||||||
3. По данным первого и последнего столбцов таблицы построить график зависимости поверхностного натяжения раствора от температуры.
 2015-01-07
2015-01-07 800
800








