Задание 10. Дляфункции 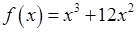 точка
точка 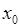 есть точка перегиба. Тогда
есть точка перегиба. Тогда 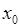 равна:
равна:
А. 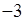
| Б. 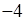
| В. 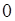
| Г. 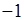
|
Решение. Непрерывная на отрезке 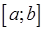 функция
функция 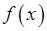 называется выпуклой вверх на этом отрезке, если для любых
называется выпуклой вверх на этом отрезке, если для любых 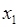 и
и 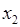 из этого отрезка
из этого отрезка
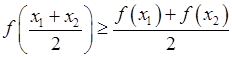 .
.
Аналогично определяется функция, выпуклая вниз.
Дважды дифференцируемая на 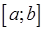 функция
функция 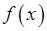 выпукла вверх, если для любого
выпукла вверх, если для любого 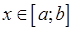
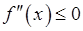 .
.
Дважды дифференцируемая на 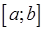 функция
функция 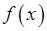 выпукла вниз, если для любого
выпукла вниз, если для любого 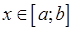
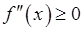 .
.
Пусть функция 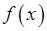 непрерывна в точке
непрерывна в точке 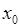 и имеет в этой точке конечную или бесконечную производную. Тогда точка
и имеет в этой точке конечную или бесконечную производную. Тогда точка 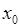 называется точкой перегиба функции
называется точкой перегиба функции 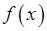 , если в этой точке изменяется направление ее выпуклости.
, если в этой точке изменяется направление ее выпуклости.
Необходимое условие наличия точки перегиба. Если 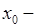 точка перегиба функции
точка перегиба функции 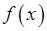 , и функция
, и функция 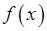 имеет вторую производную, непрерывную в этой точке, то
имеет вторую производную, непрерывную в этой точке, то 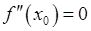 .
.
Достаточное условие наличия точки перегиба. Пусть функция 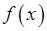 непрерывна и имеет конечную или бесконечную производную в точке
непрерывна и имеет конечную или бесконечную производную в точке 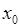 . Если
. Если 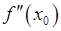 меняет знак при переходе через точку
меняет знак при переходе через точку 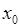 , то
, то 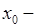 точка перегиба функции
точка перегиба функции 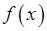 .
.
Дляфункции 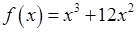 проверяем необходимое условие наличия точки перегиба.
проверяем необходимое условие наличия точки перегиба.
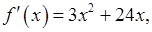
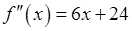
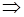
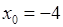 .
.
Проверяем достаточное условие наличия точки перегиба. Поскольку 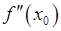 меняет знак при переходе через точку
меняет знак при переходе через точку 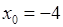 , то
, то 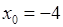 точка перегиба функции
точка перегиба функции 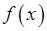 .
.
 2015-01-07
2015-01-07 202
202








