Задание 11. Функция 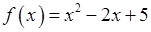 возрастает при:
возрастает при:
А. 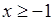
| Б. 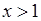
| В. 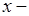 любом любом
| Г. 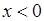
|
Решение. Функция 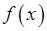 называется возрастающей на множестве
называется возрастающей на множестве 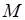 (
(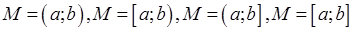 ), если для любых
), если для любых 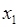 и
и 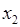 из этого множества и таких, что
из этого множества и таких, что 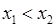 выполняется неравенство
выполняется неравенство 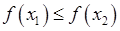 .
.
Для того чтобы дифференцируемая функция 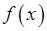 была возрастающей на множестве
была возрастающей на множестве 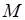 , необходимо и достаточно, чтобы её производная
, необходимо и достаточно, чтобы её производная 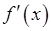 была неотрицательной на множестве
была неотрицательной на множестве 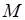 .
.
Дляфункции 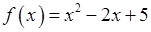 проверяем необходимое и достаточное условие возрастания на множестве
проверяем необходимое и достаточное условие возрастания на множестве 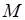 :
:
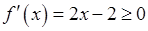
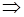
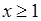 .
.
Следовательно, на множестве 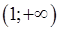 функция возрастает.
функция возрастает.
 2015-01-07
2015-01-07 288
288








