Задание 3. Найтизначениефункции 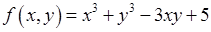 в точке локального экстремума.
в точке локального экстремума.
Решение. Точка 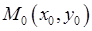 является точкой максимума (минимума) функции
является точкой максимума (минимума) функции 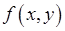 , если найдется такая окрестность точки
, если найдется такая окрестность точки 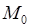 , что для всех точек
, что для всех точек 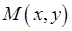 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 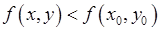
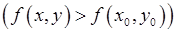 .
.
Точки максимума и минимума называются точками экстремума. При этом если в точке экстремума существует первая частная производная, по какому-либо аргументу, то она равна нулю.
Точки экстремума дифференцируемой функции, то есть функции, имеющей непрерывные частные производные во всех точках некоторой области, надо искать только среди тех точек, в которых все первые частные производные равны нулю.
Пусть 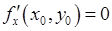 и
и 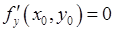 , а вторые частные производные функции
, а вторые частные производные функции 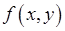 непрерывны в некоторой окрестности точки
непрерывны в некоторой окрестности точки 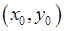 . Введем обозначения:
. Введем обозначения:
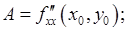
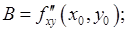
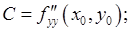
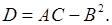
Тогда, если 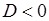 , то в точке
, то в точке 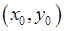 экстремума нет.
экстремума нет.
Если 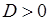 , то в точке
, то в точке 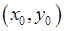 экстремум функции
экстремум функции 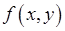 есть, причем если
есть, причем если 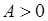 , то минимум, а если
, то минимум, а если 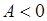 , то максимум.
, то максимум.
Если 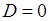 , то экстремум может быть, а может и не быть. В данном случае требуются дополнительные исследования.
, то экстремум может быть, а может и не быть. В данном случае требуются дополнительные исследования.
Для функции 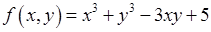 находим первые частные производные:
находим первые частные производные:
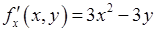 ,
, 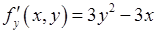
и решаем систему
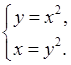
Тем самым находим точки подозрительные на экстремум: 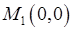 и
и 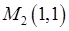 .
.
Находим вторы частные производные и смешанную производную:
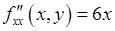 ,
, 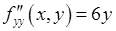 ,
, 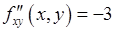 .
.
Определяем знак выражения 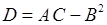 в каждой точке подозрительной на экстремум
в каждой точке подозрительной на экстремум
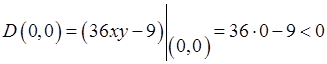 .
.
Следовательно, в точке 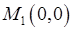 экстремума нет.
экстремума нет.
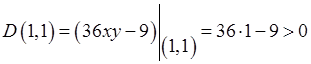 .
.
Поэтому в точке 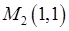 есть экстремум.
есть экстремум.
Находимзначениефункции 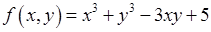 в точке
в точке 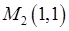 :
:
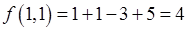
 2015-01-07
2015-01-07 299
299








