Задание 2. Найтиточку минимума функции 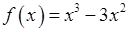 .
.
Решение. В точке 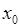 функция
функция 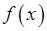 достигает экстремума - минимума (максимума), если для любых
достигает экстремума - минимума (максимума), если для любых 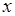 из некоторой окрестности точки
из некоторой окрестности точки 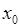 выполняется неравенство
выполняется неравенство 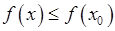
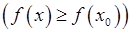 .
.
Во всех точках экстремума производная функции 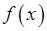 равна нулю или не существует.
равна нулю или не существует.
Пусть функция 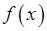 дифференцируема в некоторой окрестности точки
дифференцируема в некоторой окрестности точки 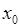 , кроме, быть может, самой точки, и непрерывна в точке
, кроме, быть может, самой точки, и непрерывна в точке 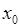 . Если производная функции меняет знак с минуса на плюс при переходе через точку слева направо, то
. Если производная функции меняет знак с минуса на плюс при переходе через точку слева направо, то 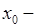 точка минимума. Если производная функции меняет знак с плюса на минус при переходе через точку слева направо, то
точка минимума. Если производная функции меняет знак с плюса на минус при переходе через точку слева направо, то 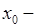 точка максимума.
точка максимума.
Для функции 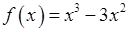 производная равна
производная равна
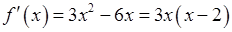 .
.
Определяем знаки производной:
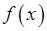
| 
| 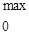
| 
| 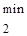
| 
|
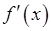
| 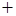
| 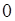
| 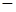
| 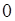
| 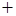
|
 2015-01-07
2015-01-07 349
349







