Система булевых функций 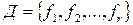 называется полной, если любую булеву функцию можно представить в виде суперпозиции функций из Д.
называется полной, если любую булеву функцию можно представить в виде суперпозиции функций из Д.
Приведем пример полных систем.
Пример 1 Как отмечено выше, система 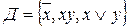 является
является
полной.
Пример 2 Множество всех булевых функций P2 является полной системой.
В вопросе о полноте важную роль играет следующая теорема.
Пусть 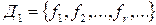 и
и 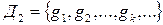 системы булевых функций. Если Д1 – полная система и каждая ее функция выражается в виде суперпозиции функций из Д2, то система Д2 также является полной.
системы булевых функций. Если Д1 – полная система и каждая ее функция выражается в виде суперпозиции функций из Д2, то система Д2 также является полной.
Действительно, так как Д1 – полная система, то любая булева функция представима в виде суперпозиции функций из Д1. А так как любая функция из Д1 представима в виде суперпозиций функций из Д2, то Д2 – полная система.
Пример 3 Система 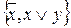 – полная.
– полная.
Это следует из предыдущей теоремы и из примера 1, ибо 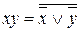 . Аналогичным образом получаем полноту системы
. Аналогичным образом получаем полноту системы 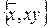 . Приведенные примеры говорят о том, что существуют различные полные системы булевых функций. Каждая из таких систем может быть принята в качестве набора «элементарных» функций, и любая булева функция может быть выражена в виде суперпозиции через «элементарные» функции принятого набора.
. Приведенные примеры говорят о том, что существуют различные полные системы булевых функций. Каждая из таких систем может быть принята в качестве набора «элементарных» функций, и любая булева функция может быть выражена в виде суперпозиции через «элементарные» функции принятого набора.
С понятием полноты тесно связано понятие замкнутого класса и замыкания.
Множество Т булевых функций называется замкнутым классом, если любая суперпозиция функций из Т снова принадлежит Т.
Всякая система М булевых функций порождает некоторый замкнутый класс. Этот класс состоит из всех булевых функций, которые можно получить суперпозициями из М. Такой класс называется замыканием М и обозначается [М]. Для замкнутого класса М следует, что [М] = М. Очевидно, что если М – полная система, что [М] = Р2.
При установлении необходимого и достаточного условия полноты важную роль играют пять замечательных классов булевых функций, которые будут рассмотрены ниже.
Первый замечательный класс – класс булевых функций, сохраняющих константу С, т.е. функций 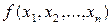 , для которых
, для которых 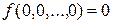 .
.
Подсчитаем число таких булевых функций от n переменных. Поскольку на нулевом наборе значение функций из Т0 фиксировано, то в Т0 содержится ровно 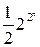 булевых функций от n переменных.
булевых функций от n переменных.
Ясно, что функции 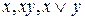 принадлежат классу Т0, а
принадлежат классу Т0, а 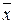 не принадлежит Т0. Следовательно,
не принадлежит Т0. Следовательно, 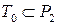 .
.
Второй замечательный класс – класс булевых функций, сохраняющих константу 1, т.е. функций 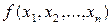 , для которых
, для которых 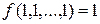 .
.
Как и выше, легко подсчитать число таких функций от переменных. Их
ровно 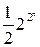 .
.
Ясно, что функции 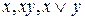 принадлежат классу Т1, а функция
принадлежат классу Т1, а функция 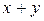 – нет. Следовательно,
– нет. Следовательно, 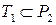 .
.
Третий замечательных класс – класс всех самодвойственных функций S.
Булева функция 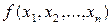 называется самодвойственной, если она совпадает со своей двойственной, т.е.
называется самодвойственной, если она совпадает со своей двойственной, т.е. 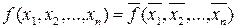 .
.
Пример 4 Доказать, что функция 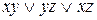 является самодвойственной.
является самодвойственной.
Двойственная для данной функции есть функция 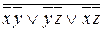 . Теперь, применяя закон де Моргана, получаем:
. Теперь, применяя закон де Моргана, получаем:
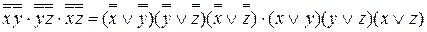
Используя законы дистрибутивности и идемпотентности, имеем:
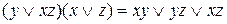
Следовательно, искомая функция самодвойственна.
Очевидно, что 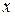 и
и 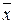 принадлежат классу S, а
принадлежат классу S, а 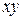 ,
, 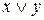 не принадлежат классу S. Следовательно,
не принадлежат классу S. Следовательно, 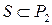 .
.
Подсчитаем число всех самодвойственных функций от n переменных.
Так как самодвойственная функция 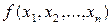 на наборах
на наборах 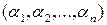 и
и 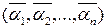 принимает противоположные значения, то она полностью определяется своими значениями, принимаемыми ею на половине всех наборов переменных. Следовательно, число самодвойственных функций от переменных равно
принимает противоположные значения, то она полностью определяется своими значениями, принимаемыми ею на половине всех наборов переменных. Следовательно, число самодвойственных функций от переменных равно 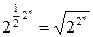 .
.
Четвертый замечательный класс – класс всех линейных булевых функций.
Булевы функции вида 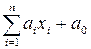 , где
, где 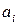 и
и 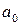 равны нулю или единице, называют линейными.
равны нулю или единице, называют линейными.
Нетрудно подсчитать число всех линейных булевых функций от переменных. Их число равно 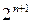 .
.
Очевидно, что функции 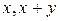 принадлежат L, а функция xy не принадлежит L. Следовательно
принадлежат L, а функция xy не принадлежит L. Следовательно 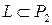 .
.
Для того, чтобы определить, является данная булева функция линейной или нет, ее надо представить в виде полинома Жегалкина.
Пример 5 Выяснить, является ли функция 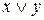 линейной. Запишем данную функцию в виде полинома Жегалкина:
линейной. Запишем данную функцию в виде полинома Жегалкина:
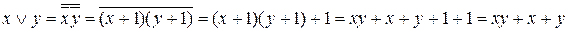 .
.
Следовательно, функция 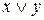 не является линейной.
не является линейной.
Пятый замечательный класс – класс М всех монотонных булевых функций.
Два набора 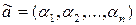 и
и 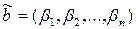 называются сравнимыми, если
называются сравнимыми, если 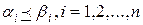 .
.
Запись 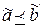 означает, что набор
означает, что набор 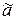 предшествует набору
предшествует набору 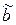 . Например,
. Например, 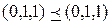 , а наборы
, а наборы 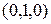 и
и 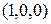 несравнимы.
несравнимы.
Булева функция 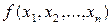 называется монотонной, если для любых наборов
называется монотонной, если для любых наборов 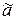 и
и 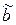 таких, что
таких, что 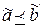 , имеет место неравенство
, имеет место неравенство 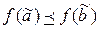 .
.
Очевидно, что константы 0,1 и функция х – монотонные функции.
Функции 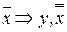 – монотонные функции (доказательство осуществляяется проверкой).
– монотонные функции (доказательство осуществляяется проверкой).
Функции 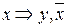 не являются монотонными, так как
не являются монотонными, так как 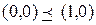 , а
, а 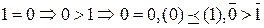 .
.
Следовательно, 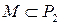 .
.
Для распознавания монотонности функции полезной является следующая теорема.
Теорема 1 Булева функция, имеющая дизъюнктивную нормальную форму, не содержащую отрицаний, является монотонной функцией, отличной от 0 и 1.
Докажем данную теорему. Пусть булева функция 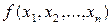 имеет дизъюнктивную нормальную форму Д, не содержащую отрицаний, и пусть на наборе
имеет дизъюнктивную нормальную форму Д, не содержащую отрицаний, и пусть на наборе 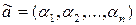 ,
, 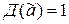 . Тогда Д содержит конъюнкцию
. Тогда Д содержит конъюнкцию 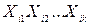 равную единице на наборе
равную единице на наборе 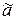 . Следовательно,
. Следовательно, 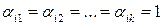 . Возьмем любой набор
. Возьмем любой набор 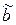 такой, что
такой, что 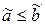 . В нем обязательно
. В нем обязательно 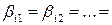
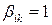 . Поэтому конъюнкция
. Поэтому конъюнкция 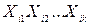 при этом наборе равна 1, а значит
при этом наборе равна 1, а значит 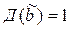 . Итак, условие монотонности для ДНФ Д выполнено. А это значит, что функция
. Итак, условие монотонности для ДНФ Д выполнено. А это значит, что функция 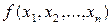 монотонна.
монотонна.
Используя данную теорему, сразу получаем, что функции 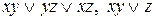 являются монотонными.
являются монотонными.
Классы булевых функций 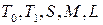 являются замкнутыми классами.
являются замкнутыми классами.
Докажем, что 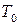 – замкнутый класс. Для этого надо показать, что функция
– замкнутый класс. Для этого надо показать, что функция 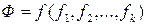 принадлежит
принадлежит 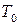 , если функция f,
, если функция f, 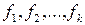 принадлежит
принадлежит 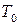 . Это следует из следующей цепочки неравенств:
. Это следует из следующей цепочки неравенств:
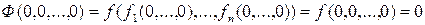 .
.
Аналогичным образом доказывается замкнутость класса 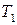 .
.
Если 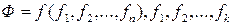 самодвойственные функции, то
самодвойственные функции, то 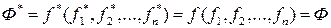 . Итак, S – замкнутый класс.
. Итак, S – замкнутый класс.
Пусть 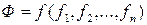 , где
, где 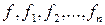 – монотонные функции, и
– монотонные функции, и
пусть 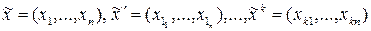 их наборы переменных. Здесь переменные функции Ф состоят из функций
их наборы переменных. Здесь переменные функции Ф состоят из функций 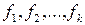 . Пусть
. Пусть 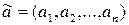 и
и 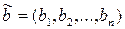 два таких набора, что
два таких набора, что 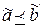 . Каждый из наборов
. Каждый из наборов 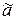 и
и 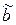 однозначно определяет следующие наборы
однозначно определяет следующие наборы 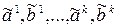 значений переменных
значений переменных 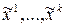 . Причем
. Причем 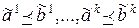 . Так как
. Так как 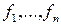 – монотонные функции, то
– монотонные функции, то 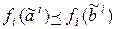 . Следовательно,
. Следовательно, 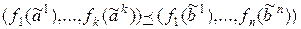 . Из монотонности функции f получаем, что
. Из монотонности функции f получаем, что 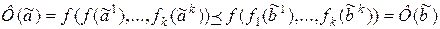 .
.
Итак, М – замкнутый класс.
Замкнутость класса L следует непосредственно из определения линейных функций.
Как показано выше, функция 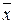 не принадлежит классу М. Следующая теорема показывает, что всякая немонотонная функция содержит, в некотором смысле, в своем составе функцию отрицания.
не принадлежит классу М. Следующая теорема показывает, что всякая немонотонная функция содержит, в некотором смысле, в своем составе функцию отрицания.
Теорема 2 Если 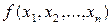 – немонотонная функция, то в результате ее суперпозиции с константами 0 и 1 может быть получена функция отрицания
– немонотонная функция, то в результате ее суперпозиции с константами 0 и 1 может быть получена функция отрицания 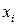 одного из аргументов функции
одного из аргументов функции 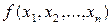 .
.
Докажем данную теорему. Так как функция 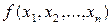 немонотонная, то найдутся два набора
немонотонная, то найдутся два набора 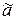 и
и 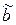 значений переменных таких, что
значений переменных таких, что 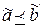 , и
, и 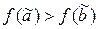 . Причем, в качестве этих наборов
. Причем, в качестве этих наборов 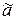 и
и 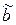 можно выбрать соседние наборы, т.е. наборы, отличающиеся значениями только по одной из координат. Действительно, если
можно выбрать соседние наборы, т.е. наборы, отличающиеся значениями только по одной из координат. Действительно, если 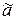 и
и 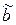 не являются соседними наборами, то набор
не являются соседними наборами, то набор 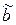 отличается от набора
отличается от набора 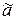 в t координатах, где t > 1. Причем, эти координаты в наборе
в t координатах, где t > 1. Причем, эти координаты в наборе 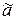 равны 0, а в наборе
равны 0, а в наборе 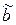 равны 1. Из этого следует, что между наборами
равны 1. Из этого следует, что между наборами 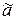 и
и 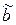 можно вставить t – 1 наборов
можно вставить t – 1 наборов 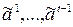 , таких, что
, таких, что
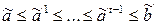 . (4.1)
. (4.1)
Так как 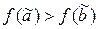 , то обязательно найдется такая пара соседних наборов из цепочки (4.1)
, то обязательно найдется такая пара соседних наборов из цепочки (4.1) 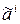 и
и 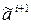 , что
, что 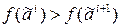 . Не ограничивая общности, мы можем считать, что
. Не ограничивая общности, мы можем считать, что 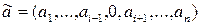 ;
;
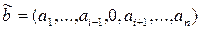 .
.
Подставим в функцию 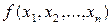 вместо переменной
вместо переменной 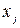 константу
константу 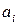 , где
, где 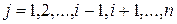 . В результате мы получим функцию от одной переменной:
. В результате мы получим функцию от одной переменной: 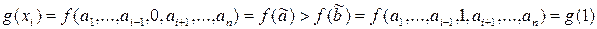
А это значит, что 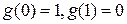 . Следовательно,
. Следовательно, 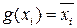 .
.
 2014-09-02
2014-09-02 8172
8172
