Определение 17 Две формулы 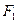 и
и 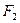 алгебры логики предикатов называются равносильными на множестве М, если при любой подстановке в эти формулы вместо предикатных переменных любых конкретных предикатов, определённых на множестве М, формулы превращаются в равносильные предикаты. Если две формулы равносильны на любых множествах, то их будем называть просто равносильными и обозначать
алгебры логики предикатов называются равносильными на множестве М, если при любой подстановке в эти формулы вместо предикатных переменных любых конкретных предикатов, определённых на множестве М, формулы превращаются в равносильные предикаты. Если две формулы равносильны на любых множествах, то их будем называть просто равносильными и обозначать 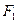 =
= 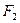 .
.
В следующих теоремах приводятся наиболее важные равносильные формулы алгебры логики предикатов.
Теорема 8 (законы де Моргана для кванторов) Следующие формулы алгебры логики предикатов равносильны:
1) 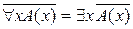 ;
;
2) 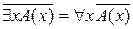 ;
;
Доказательство. 1) Пусть А(х) – произвольный конкретный одноместный предикат, определённый на произвольном множестве М. Тогда 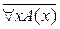 и
и 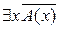 – высказывания.
– высказывания.
Пусть 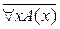 =1. Тогда
=1. Тогда 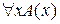 =0. Отсюда следует, что А(х)
=0. Отсюда следует, что А(х)  1. А это значит, что
1. А это значит, что 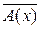
 0. Теперь согласно определению 12
0. Теперь согласно определению 12 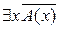 =1.
=1.
Пусть 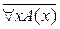 =0. Тогда
=0. Тогда 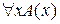 =1. Отсюда следует, что А(х)
=1. Отсюда следует, что А(х) 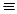 1. А это значит, что
1. А это значит, что 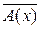
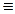 0. Теперь, согласно определению 12
0. Теперь, согласно определению 12 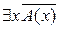 = 0.
= 0.
Доказательство определения 2) приводится аналогично.
Следствие. Следующие формулы алгебры логики предикатов равносильны: 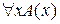 =
= 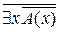
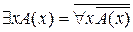
Действительно, согласно теореме 8 и закону двойного отрицания получаем 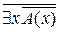 =
= 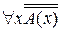 =
= 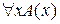 .
.
Теорема 9 (законы пронесения кванторов через конъюнкцию) Следующие формулы алгебры логики предикатов равносильны:
1 ) 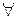 x(A (x) ·B (x))=(
x(A (x) ·B (x))=(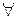 xA (x))·(
xA (x))·(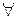 xB (x));
xB (x));
2) 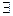 x (A (x)· P)=(
x (A (x)· P)=(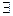 xA (x))· P.
xA (x))· P.
Доказательство. 1) Пусть А(х),В(х) – произвольные одноместные предикаты, определённые на произвольном множестве М. Пусть 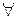 x(А(х)·В(х)) =1. Тогда А(х)·В(х) ≡ 1. Согласно следствию из теоремы 2 А(х) ≡ 1 и В(х) ≡ 1 одновременно. Согласно определению 11
x(А(х)·В(х)) =1. Тогда А(х)·В(х) ≡ 1. Согласно следствию из теоремы 2 А(х) ≡ 1 и В(х) ≡ 1 одновременно. Согласно определению 11 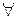 xA (x) = 1 и
xA (x) = 1 и 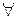 xВ (x) = 1. А это значит, что (
xВ (x) = 1. А это значит, что (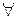 xA (x))·(
xA (x))·(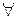 xB (x)) = 1.
xB (x)) = 1.
Пусть теперь 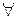 x (А (х)· В (х)) = 0. Тогда согласно определению 11
x (А (х)· В (х)) = 0. Тогда согласно определению 11
А(х)·В(х)  1. Согласно следствию из теоремы 2 либо А(х)
1. Согласно следствию из теоремы 2 либо А(х)  1, либо
1, либо
В(х)  1. Но тогда согласно определению 11 либо
1. Но тогда согласно определению 11 либо 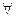 xA (x) = 0, либо
xA (x) = 0, либо 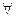 xВ (x) = 0. А это значит, что (
xВ (x) = 0. А это значит, что (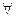 xA (x))·(
xA (x))·(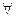 xB (x)) = 0.
xB (x)) = 0.
2) Пусть А(х) – произвольный конкретный одноместный предикат, определённый на множестве М, а Р – произвольное конкретное высказывание.
Пусть 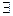 x (А (х)· Р) = 1. Согласно определению 12 А(х)·Р
x (А (х)· Р) = 1. Согласно определению 12 А(х)·Р  0. Отсюда нетрудно заметить, что А(х)
0. Отсюда нетрудно заметить, что А(х)  0 и Р =1. Тогда согласно определению 12
0 и Р =1. Тогда согласно определению 12 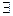 xА(х) = 1. А это значит, что (
xА(х) = 1. А это значит, что (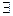 xА (х))· Р = 1.
xА (х))· Р = 1.
Пусть 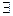 x (А (х)· Р) = 0. Тогда согласно определению 12 А(х)·Р ≡ 0. Но тогда либо А(х) ≡ 0, либо Р = 0. А это значит, что либо
x (А (х)· Р) = 0. Тогда согласно определению 12 А(х)·Р ≡ 0. Но тогда либо А(х) ≡ 0, либо Р = 0. А это значит, что либо 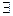 xА(х) = 0, либо Р =0. Отсюда следует, что (
xА(х) = 0, либо Р =0. Отсюда следует, что (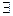 xA (x))· P = 0. Теорема доказана.
xA (x))· P = 0. Теорема доказана.
Покажем, что квантор общности через дизъюнкцию проносить нельзя, т.е. 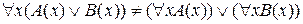 .
.
Действительно, пусть А(х) – «х нечётное число», а В(х) – «х чётное число» два предиката, определённые на множестве натуральных чисел. Тогда 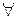 x (А (х)Ú В (х)) – истинное высказывание «любое натуральное число либо чётно, либо нечётно».
x (А (х)Ú В (х)) – истинное высказывание «любое натуральное число либо чётно, либо нечётно». 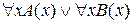 – ложное высказывание «любое натуральное число нечётно или натуральное число чётно».
– ложное высказывание «любое натуральное число нечётно или натуральное число чётно».
Теорема 10 (законы пронесения кванторов через дизъюнкцию) Следующие формулы алгебры логики предикатов равносильны:
1 ) 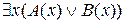 =
= 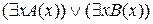 ;
;
2 ) 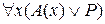 =
= 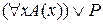 ;
;
Доказательство. Пусть А(х), В(х) – произвольные конкретные одноместные предикаты, определённые на произвольном множестве М, а Р – произвольное конкретное высказывание.
1) Пусть 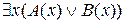 = 1. Тогда
= 1. Тогда 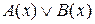
 0. Согласно следствию из теоремы 3 либо А(х)
0. Согласно следствию из теоремы 3 либо А(х)  0, либо В(х)
0, либо В(х)  0 одновременно. Согласно определению 12 либо
0 одновременно. Согласно определению 12 либо 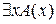 =1, либо
=1, либо 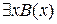 =1. А это значит, что
=1. А это значит, что 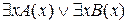 = 1.
= 1.
Пусть теперь 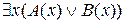 = 0. Тогда согласно определению 12
= 0. Тогда согласно определению 12 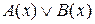 ≡ 0. По следствию из теоремы 3 А(х) ≡ 0 и В(х) ≡ 0. Согласно определению 12
≡ 0. По следствию из теоремы 3 А(х) ≡ 0 и В(х) ≡ 0. Согласно определению 12 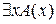 = 0 и
= 0 и 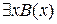 = 0. А это значит, что
= 0. А это значит, что 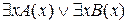 = 0.
= 0.
2) Пусть 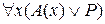 = 1. Тогда согласно определению 11
= 1. Тогда согласно определению 11 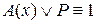 . А это значит, что либо А(х) ≡1, либо Р = 1. Отсюда либо
. А это значит, что либо А(х) ≡1, либо Р = 1. Отсюда либо 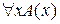 = 1, либо
= 1, либо
Р = 1. В любом случае 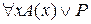 = 1.
= 1.
Пусть теперь 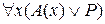 = 0. Тогда согласно определению 11
= 0. Тогда согласно определению 11 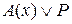
 1. Отсюда следует, что Р =0 и А(х)
1. Отсюда следует, что Р =0 и А(х)  1. Но тогда Р = 0 и
1. Но тогда Р = 0 и 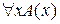 = 0. Следовательно,
= 0. Следовательно, 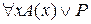 = 0. Теорема доказана.
= 0. Теорема доказана.
Покажем, что квантор существования через конъюнкцию проносить нельзя, т. е. 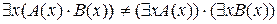 .
.
Пусть А(х) = (x >2), определённый на R и В(х) = (х <2 ), определённый на R. Тогда 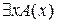 = 1 и
= 1 и 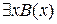 = 1. Следовательно, (
= 1. Следовательно, (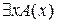 )·(
)·(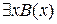 ) = 1. Очевидно, что
) = 1. Очевидно, что 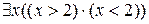 = 0.
= 0.
Теорема 11 (законы пронесения кванторов через импликацию) Следующие формулы алгебры логики предикатов равносильны:
1) 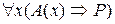 =
= 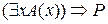 ;
;
2) 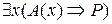 =
= 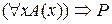 ;
;
3) 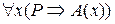 =
= 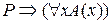 ;
;
4) 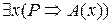 =
= 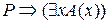 ;
;
Доказательство. Пусть А(х) – произвольный конкретный одноместный предикат, определённый на множестве М, а Р – произвольное конкретное высказывание.
1) Пусть 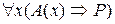 = 1. Тогда согласно определению 11
= 1. Тогда согласно определению 11 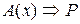 ≡1. Отсюда нетрудно показать, что либо А(х) ≡ 0, либо Р = 1. А это значит, что либо
≡1. Отсюда нетрудно показать, что либо А(х) ≡ 0, либо Р = 1. А это значит, что либо 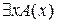 = 0, либо Р = 1. В любом из этих случаев
= 0, либо Р = 1. В любом из этих случаев 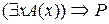 = 1.
= 1.
Пусть теперь 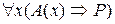 = 0. Тогда согласно определению 11
= 0. Тогда согласно определению 11 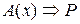
 1. А это значит, что А(х)
1. А это значит, что А(х)  1 и Р = 0. Тогда
1 и Р = 0. Тогда 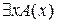 = 1 и Р = 0. Отсюда
= 1 и Р = 0. Отсюда 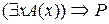 = 0.
= 0.
2 ) Пусть 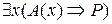 = 1. Тогда согласно определению 11
= 1. Тогда согласно определению 11 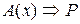
 0. Тогда либо Р = 1, либо А(х)
0. Тогда либо Р = 1, либо А(х)  1. В любом случае
1. В любом случае 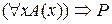 = 1.
= 1.
Пусть теперь 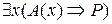 = 0. Тогдасогласно определению 12
= 0. Тогдасогласно определению 12 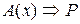 ≡0. А это значит, что А(х) ≡ 1 и Р = 0. Отсюда
≡0. А это значит, что А(х) ≡ 1 и Р = 0. Отсюда 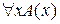 = 1 и Р = 0. А это значит, что
= 1 и Р = 0. А это значит, что 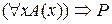 = 0.
= 0.
3) Пусть 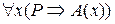 =1. Тогда согласно определению 11
=1. Тогда согласно определению 11 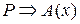 ≡1. Отсюда либо Р = 0, либо А(х)
≡1. Отсюда либо Р = 0, либо А(х)  1. Следовательно, либо
1. Следовательно, либо
Р = 0, либо 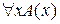 = 1. В любом случае
= 1. В любом случае 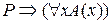 = 1.
= 1.
Пусть теперь 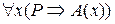 = 0. Тогда согласно определению 11
= 0. Тогда согласно определению 11 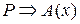
 1. Тогда Р = 1 и А(х)
1. Тогда Р = 1 и А(х)  1. Отсюда Р = 1 и
1. Отсюда Р = 1 и 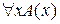 = 0. Следовательно
= 0. Следовательно 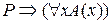 = 0.
= 0.
4) Пусть 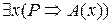 = 1. Тогда согласно определению 12
= 1. Тогда согласно определению 12 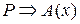
 0. Отсюда либо Р = 0, либо А(х)
0. Отсюда либо Р = 0, либо А(х)  0. Следовательно, либо
0. Следовательно, либо
Р = 0, либо 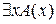 =1. А это значит, что существует
=1. А это значит, что существует 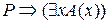 = 1.
= 1.
Пусть теперь 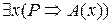 = 0. Тогда согласно определению 12
= 0. Тогда согласно определению 12 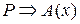 ≡ 0. Отсюда Р = 1 и А(х) ≡ 0. Следовательно Р = 1 и
≡ 0. Отсюда Р = 1 и А(х) ≡ 0. Следовательно Р = 1 и 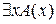 = 0. А это значит, что
= 0. А это значит, что 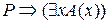 = 0. Теорема доказана.
= 0. Теорема доказана.
Теорема 12 (законы коммутативности для кванторов): Следующие формулы алгебры логики предикатов равносильны:
1) 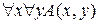 =
= 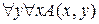 ;
;
2) 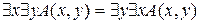 .
.
Доказательство непосредственно следуют из определений 11 и 12.
Пример 1 Доказать, что следующая формула 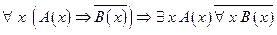 является тавтологией.
является тавтологией.
Доказательство. Пусть A (x)и B (x) ― произвольные конкретные предикаты, определённые на множестве M. Подставим их в исходную формулу, в результате получим высказывание. Покажем, что данное высказывание истинно.
Способ 1 Предположим противное. Пусть 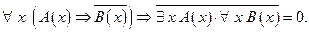
Согласно определению импликации:
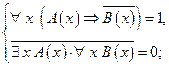 Отсюда следует, что
Отсюда следует, что 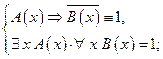
Тогда
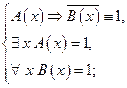 Отсюда
Отсюда 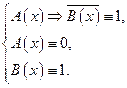 Но тогда
Но тогда 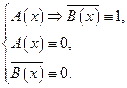
Отсюда следует, что существует такое значение x 0 из M, что 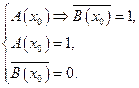
Получим противоречие. Следовательно, искомая формула является тавтологией.
Способ 2 Известно, что 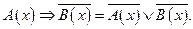
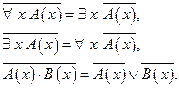 Тогда
Тогда 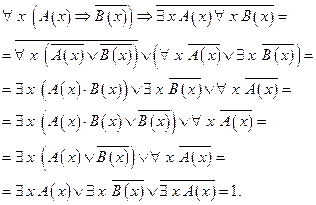
Вопросы для самоконтроля
1 Дайте определение 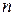 -местного предиката.
-местного предиката.
2 Дайте определение тождественно истинного предиката, приведите примеры.
3 Дайте определение тожественно ложного предиката, приведите примеры.
4 Дайте определение выполнимого предиката, приведите примеры.
5 Дайте определение операции применения квантора общности.
6 Дайте определение операции применения квантора существования.
7 Дайте определение формулы логики предикатов.
8 Что называется интерпретацией формулы логики предикатов?
9 Какие формулы логики предикатов называются замкнутыми?
10 Какие формулы логики предикатов называются открытыми?
11 Дайте определение выполнимой формулы логики предикатов.
12 Дайте определение тавтологии.
13 Дайте определение противоречия.
14 Что можно сказать о проблеме разрешимости в алгебре логики предикатов?
15 Какие формулы алгебры логики предикатов называются равносильными?
16 Сформулируйте законы де Моргана для кванторов.
17 Сформулируйте законы пронесения кванторов через конъюнкцию.
18 Сформулируйте законы пронесения кванторов через дизъюнкцию.
19 Сформулируйте законы пронесения кванторов через импликацию.
20 Сформулируйте законы коммутативности для кванторов.
 2014-09-02
2014-09-02 3735
3735
