Детерминированные функции

Обозначим через 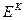={0, 1, …, k-1}, где k – некоторое натуральное число, а через 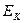множество всех k-значных последовательностей a таких, что а = { a (1), a (2),…, a (t), …}, где a (i)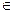 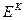для всех I = 1, 2,….

Обозначим через 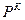множество всех функций y = f 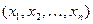, определённых на наборах 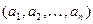, где 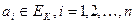и принимающих значение из 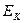. Функции из 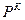преобразуют наборы k-значных последовательностей в k-значные последовательности. В множество 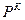включим также все последовательности из 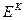, рассматривая их как функции, зависящие от пустого множества переменных, т. е. как константы.

С помощью векторной записи функции от n переменных из 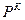можно свести к функции от одной переменной. Обозначим набор переменных 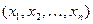через Х, вместо y = f 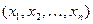будем писать y = f (Х). При этом значение переменной Х, есть вектор а = 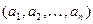компонентами которого являются последовательности из 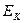, 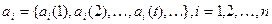. Будем рассматривать а как последовательность векторов 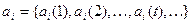, где .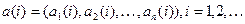

Таким образом, мы будем считать, что выполняется тождество: =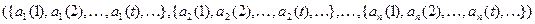

= .

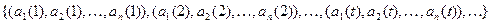Лемма 1 Число наборов 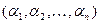, где 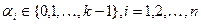равно .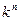

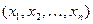
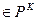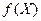
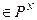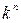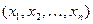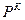Итак, функцию y = f с помощью векторной записи можно свести к функции y = , где N = . Таким образом, изучение функции y = f из можно свести к изучению функции от одной переменной из 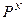, где N = .

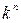Определение 1 Функция y = 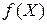из 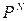называется детерминированной, если каково бы ни было число t и каковы бы ни были последовательности а и b такие, что a(1)=b(1), a(2)=b(2), … a(t)=b(t) значения функций α, β, где α= 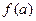, β= 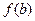представляют собой последовательности, у которых тоже совпадают первые t членов, т. е. α(1) = β(1), α(2) = β(2), …, α(t) = = β(t).

Множество всех детерминированных функций обозначим через .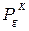

Из определения детерминированной функции следует, что значение α (t) (α= 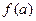) зависит только от значения первых t членов входной последовательности а, т. е. а(1), а(2), …, а(t), следовательно α(t)=φ(а(1), а(2), …, а(t)).

Приведём примеры как детерминированных, так и недетерминированных функций.

Пример 1 Рассмотрим функцию y = 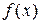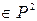, определённую следующим образом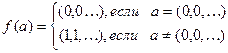

Покажем, что данная функция недетерминированная. Действительно, возьмём две входные последовательност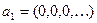и и 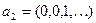. Тогда 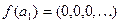и 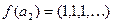. Следовательно, данная функция недетерминированная.

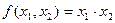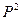Пример 2 Рассмотрим функцию из , определённую следующим образом 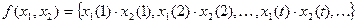.Здесь выходная последовательность – почленная конъюнкция входных последовательностей. Очевидно, что .

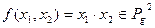Пример 3 Рассмотрим функцию z = x + y 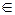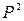, осуществляющую сложение 2-значных последовательностей в двоичной системе с бесконечным числом разрядов. Для этого используется обычный алгоритм сложения двух чисел столбиком

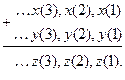
Очевидно, что z(t) определяется по первым t слагаемых, т. е. x + y .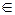

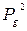Детерминированная функция 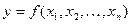может быть проинтерпретирована следующим образом. Пусть мы имеем некоторый «дискретный преобразователь», в котором существует n входов 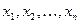и один выход .

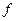На входы в моменты времени t = 1,2, …, m, … подаются входные последовательности

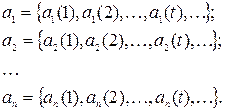
И в эти же моменты t на выходе возникает выходная последовательность 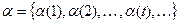, причем 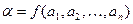. Очевидно, что в дискретном преобразователе значения α(t) зависит только от значений входных последовательностей в момент времени 1,2, …, t и не зависит от значений в будущие моменты времени. Поэтому преобразование 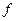есть детерминированная функция.