Рассмотренные законы алгебры логики и соотношения 0 и1 позволяют производить равносильные преобразования логических функций, т.е. получать из исходных функций более простые, содержащие меньшее число переменных, и равносильные по своему действию исходным.
Преобразование логических функций используется при анализе, синтезе и логическом контроле ДУ. Мощным аппаратом для равносильных преобразований являются так называемые основные формулы равносильных преобразований.
Относительно умножения:
1) 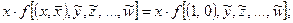
2) 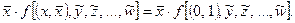
Символом ~ над переменной обозначаем, что имеется в виду и нормальная, и инверсная переменные: 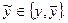
Из формул видно, что если переменная 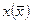 логически умножается на функцию f, то в этой функции все одноименные переменные
логически умножается на функцию f, то в этой функции все одноименные переменные 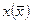 заменяются на 1, а все инверсные
заменяются на 1, а все инверсные 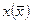 – на 0.
– на 0.
Примеры:
1) 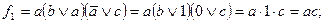
2) 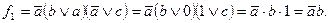
Приведенные формулы можно заменить одной:
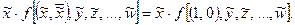
Относительно сложения:
1) 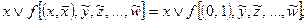
2) 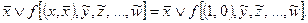
Если переменная 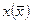 логически складывается с функцией f, то в этой функции все одноименные переменные
логически складывается с функцией f, то в этой функции все одноименные переменные 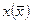 заменяются на 0, а все инверсные
заменяются на 0, а все инверсные 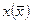 – на 1.
– на 1.
Эти формулы можно заменить одной:
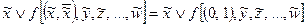
Основные формулы равносильных преобразований доказываются методом подстановки в них вместо переменной x ее возможных значений 0 и 1 и сравнения правой и левой частей уравнения.
Докажем, например, формулу
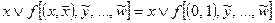 .
.
Пусть x = 0, тогда 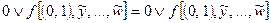 – равенство справедливо. Пусть x = 1, тогда
– равенство справедливо. Пусть x = 1, тогда 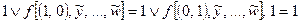 – равенство справедливо.
– равенство справедливо.
Таким образом, формула доказана.
Аналогичным образом доказываются и другие основные формулы равносильных преобразований.
Примеры:
1) 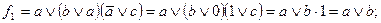
2) 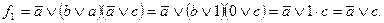
Таким образом, полученные формулы наряду с законами алгебры логики позволяют производить равносильные преобразования логических функций.
Рассмотрим некоторые примеры.
1. Упростить логическую функцию
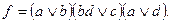
Применяем законы алгебры логики (2 раза распределительный закон) и получаем:
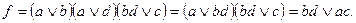
2. Упростить функцию
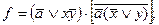


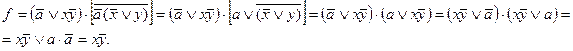
3. Упростить функцию
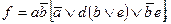
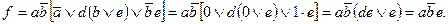
4. Упростить функцию
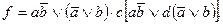
Заметим, что 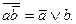 Принимая
Принимая 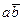 за один символ, получаем:
за один символ, получаем:
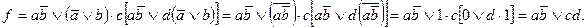
 2014-02-13
2014-02-13 940
940








