Смешанным произведением трёх векторов 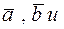
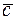 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора 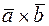 на
на 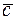
Смешанное произведение обозначается 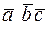 .
.
Таким образом 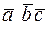 =
= 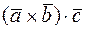
Свойства смешанного произведения:
1. 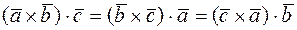 -смешанное произведение не меняется при циклической перестановке векторов;
-смешанное произведение не меняется при циклической перестановке векторов;
2. 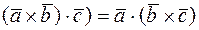 -смешанное произведение не меняется при перестановке знаков векторного и скалярного умножения;
-смешанное произведение не меняется при перестановке знаков векторного и скалярного умножения;
3. 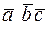 =
= 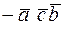 =
= 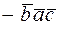 =
= 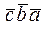 смешанное произведение меняет знак на противоположный при перемене мест любых двух векторов- сомножителей;
смешанное произведение меняет знак на противоположный при перемене мест любых двух векторов- сомножителей;
4. 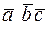 = 0, если
= 0, если 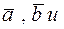
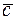 компланарны (в частности, если любые два из перемножаемых векторов коллинеарны).
компланарны (в частности, если любые два из перемножаемых векторов коллинеарны).
Если векторы заданы своими координатами 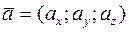
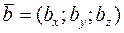 и
и 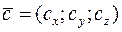 , то
, то
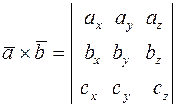
 2015-01-21
2015-01-21 252
252







