2014-09-04
1224
При программировании некоторых задач возникает необходимость использовать разложение на циклы в качестве внутреннего представления перестановки. Наиболее часто программисты используют представление, в котором начало каждого цикла определяется специальной разметкой, например, отрицательными значениями:
f = [3 1 6 7]×[5 4]×[2] = [-3 1 6 7-5 4-2].
В этом случае описание типа перестановки должно выглядеть так:
tpc= array [1..n] of -n..n;
Упражнение. 1.Опишите верификационную функцию абстрактного типа TPC с заголовком:
function TYPEC (var f: TPC): Boolean;
У к а з а н и е. Здесь нужно проверить, что модуль всех значений элементов перестановки должны быть различны и что первый элемент отрицательный.
2. Напишите процедуру:
procedure TRSL(var f: TPE; var g: TPC);
переводящую перестановку f из естественной формы в циклическую (перестановка g).
Среди алгоритмов, связанных с выполнением операций суперпозиции и нахождение обратной перестановки, наиболее интересным, является алгоритм вычисления g(f) в случае, когда f представлена в естественной форме, а g - в циклической. При этом считаем, что результат этой суперпозиции формируется на месте перестановки f.
|
|
|
Разберем этот алгоритм сначала на примере.
Пусть f=<3 5 6 2 4 7 1>, g=[-6 2 3 -5 4 1 7], тогда для вычисления g(f) обычно поступают следующим образом. Элемент 1 в f переходит в 3, а в g элемент 3 отображается в 6, т. е. в перестановке g(f) 1 сопоставляется значение 6. Далее, элемент 2 в f переходит в 5, а в g элемент 5 отображается в 4, т. е. в g(f) 2 сопоставляется значение 4. В общем случае для sÎ1,...,n выбираем значение f(s), затем совершаем поиск месторасположение значение f(s) в g; выясняем, в какое значение переходит f(s) в g и сопоставляем аргументу s значение g(f(s)). Непосредственная реализация этого алгоритма требует:
1) поиск индекса значения f(s) в массиве, соответствующем перестановке g;
2) если значение f(s) в массиве g записано последним элементом цикла, к которому принадлежит f(s), то необходимо совершить поиск индекса первого элемента этого цикла для того, чтобы вычислить g(f(s)).
Заметим, что выбор значения s можно производить произвольным образом. В частности так, что f(s) принимает значение g(n), g(n-1),...,g(1). При таком переборе значений s элементы циклов, записанные в массиве g последними, всегда обрабатываются раньше элементов этих же циклов записанных первыми. Поэтому формирование значений g(f) для s, соответствующих последним элементам циклов g, может производиться при обработке первых элементов этих же циклов. С другой стороны, такой перебор ничем не хуже перебора, когда s принимает значения 1,...,n, так как при одном подходе нам необходимо по значению s определять индекс f(s) в массиве g, а при другом подходе по значению g(i), i меняется n, n-1,...,1, определять индекс этого значения в массиве f.
|
|
|
Реализация такого алгоритма на языке Паскаль может выглядеть так:
procedure U(var f:TPE; var g: TPC); {f=g×f}
var i,j,k,s: 0..n;
begin k:=0; {0 помечает последние элементы циклов g}
{3} for i:=n downto 1 do
begin j:= abs(g[i]);
{2} s:=1; while j<> f[s] do s:=s+1;
f[s]:=k;
if g[i]<0 then
begin
{1} s:= 1; while f[s] <> 0 do s:=s+1;
f[s]:=j; k:=0
end
else k:=j
end
end;
Комментарий. Переменная i служит для перебора элементов g; k определяет значение, заносимое в f на текущем шаге; j - значение, корректируемое в f на текущем шаге; s - индекс элемента j в f.
Замечание. В процессе исполнения процедуры U элементы массива f могут принимать нулевые значения, что, вообще говоря, недопустимо по описанию абстрактного типа TPE. Однако, мы будем допускать такого рода неточности, когда при исполнении процедуры допускается расширение множества значений типа, каждый раз оговаривая подобные случаи. При этом считаем, что такие расширения недопустимы на входе и выходе процедуры.
Нетрудно видеть, что временная вычислительная сложность этого алгоритма есть О (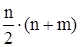
), если считать месторасположение конкретных значений элементов равновероятным; m - число циклов в перестановке. Оценим число циклов в перестановке.
ТЕОРЕМА 2. Общее число циклов во всех n! перестановках
n-го порядка равно n!´Hn, где Hn=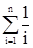 
.
Доказательство. Пусть все n! перестановок записаны в циклической форме. Зафиксируем i, 1£i£n, и рассмотрим, сколько циклов длины i встречается во всех этих перестановках.
Заметим, что конкретный цикл [a1,...,ai] встречается в (n-i)! перестановках, так как это число способов, которыми можно переставить оставшиеся n-i элементов.
Число различных возможных циклов [a1,...,ai] есть n´(n-1)´¼´(n-i)/i, так как элемент a1 можно выбрать n способами, элементами a2 - (n-1) способами и т. д.; а среди n´(n-1)´¼´(n-i+1) циклов из a1,...,ai фиксированных элементов появляется i раз, как [а1,...,аi], [a2,...,ai,a1],...,[ai,a1,...,ai-1]. Поэтому общее число циклов из i элементов во всех n! перестановках есть n´(n-1)´¼´(n-i+1)/i, взятое (n-i)! раз, т. е. n!/i.
Суммируя по всем i, получаем общее число циклов во всех n! перестановках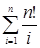 
=n!´Hn.
Таким образом, временная вычислительная сложность алгоритма U есть n´(n+Hn)/2.
Следствие. Из теоремы 2 следует, что на одну перестановку в среднем приходится Hn циклов.
Упражнение. Модернизируйте алгоритм U так, чтобы исключить поиск в f индекса нулевого значения (строка {1}).
Алгоритм U может быть использован для преобразования перестановки g из циклической формы в естественную. Для этого достаточно выполнить U, задав начальное значение f единичной перестановкой.
Замечание. Для случая преобразования перестановки g в естественную форму алгоритм U может быть упрощен за счет удаления операторов ассоциативного поиска в f индекса j (строка {2}). Проведя две указанные модернизации, можно построить алгоритм перевода с вычислительной сложностью О (n).
Упражнение. Реализуйте подобный алгоритм.
Рассмотрим алгоритм вычисления обратной перестановки для перестановок, заданных в циклической форме. Учитывая, что обратная перестановка получается за счет переориентации ребер графа перестановки, заметим, что обратная перестановка в циклической форме может быть построена путем ‘симметричного отражения перестановки относительно ее конца’, исключая начальный знак ‘ - ’.
Например, f=[-6 2 3 -5 4 1 7]: [-7 1 4 5 -3 2 6]=f-1.
Алгоритм, реализующий этот процесс, может быть представлен таким образом:
procedure O2(var f:TPC);
var i: 1..n; k: -n..n;
begin f[1]:=-f[1];
for i:=2 to n do
if f[i]<0 then begin f[i]:=-f[i]; f[i-1]:=f[i-1] end;
for i:=1 to n div 2 do
begin k:=f[i]; f[i]:=f[n-i+1]; f[n-i+1]:=k end;
f[1]:=-f[1]
end;
Упражнение. Перепишите алгоритм U, чтобы он выполнял вычисление g-1×f. У к а з ан и е. Обратите внимание на оператор {3}.
Алгоритм определения знака для перестановок, заданных в циклической форме, легко реализуется на основе теоремы 1:
|
|
|
function ч2 (var f: TPC): Boolean;
var i: 1..n; s: Boolean;
begin s:=true;
for i:=1 to n do
if f[i]>0 then s:= not s;
ч2:=s
end;
Оба алгоритма О2 и Ч2 имеет временную сложность О (n).
Наряду с представлением перестановок в циклической форме с помощью разметки начала циклов, возможна несколько иная форма представления циклических перестановок.
Определение. Будем говорить, что перестановка, представленная в виде разложения на циклы, находится в канонической форме, если:
а) обязательно записываются все циклы;
б) в каждом цикле первым записывается элемент с наименьшим значением;
в) циклы располагаются в порядке убывания значений первых элементов.
Например, f=[3 1 6 7]×[5 4] представляется как [4 5]×[2]×[1 6 7 3].
Скобочная структура в канонической форме может быть опущена, так как первым элементам циклов соответствуют левосторонние локальные минимумы (ak, i£k£n, является левосторонним локальным минимумом f, если ai<ai, 1£i<k).
В приведенном примере перестановка f может быть записана как (4 5 2 1 6 7 3), где круглые скобки указывают, что перестановка представлена в канонической форме.
Упражнение. Пусть f=<a1... an>, g=(a1... an),n¹1. Докажите, что f¹g.
Абстрактный тип ‘перестановка в канонической форме’-(TPK) на языке Паскаль может быть описан так
tpk= array [1..n] of 1..n; {описание типа }
и верификационной функцией, совпадающей с верификационной функцией представления перестановок в естественной форме (function TYPEE была описана выше). Заметим, что абстрактные типы TPE и TPK имеют различные семантики.
Рассмотрим алгоритм перевода из естественного представления перестановки в каноническую форму:
procedure CANON(var f: TPE; var g: TPK);
var i,j: 0..n;
a: array [1..n] of Boolean;
procedure B(k: integer);
begin a[k]:=false; {1}
if k<>i then
begin
B(f[k]);
g[j]:=k; j:=j-1; {2}
end
end;
begin for i:=1 to n do a[i]:=true; j:=n;
for i:=1 to n do
if a[i] then
begin {3}
B(f[i]);
g[j]:=i; j:=j-1 {4}
end
end;
Тест: f=<6 2 1 5 4 7 3>
| {3} | i=1 | j=7 | ||
| {1} | i=1 | j=7 | k=6 | a[6]=false |
| {1} | i=1 | j=7 | k=7 | a[7]=false |
| {1} | i=1 | j=7 | k=3 | a[3]=false |
| {1} | i=1 | j=7 | k=1 | a[1]=false |
| {2} | i=1 | j=6 | k=3 | g[7]=3 |
| {2} | i=1 | j=5 | k=7 | g[6]=7 |
| {2} | i=1 | j=4 | k=6 | g[5]=6 |
| {4} | i=1 | j=3 | g[4]=1 | |
| {3} | i=2 | j=3 | ||
| {1} | i=2 | j=3 | k=2 | a[2]=false |
| {4} | i=2 | j=2 | g[3]=2 | |
| {3} | i=4 | j=2 | ||
| {1} | i=4 | j=2 | k=5 | a[5]=false |
| {1} | i=4 | j=2 | k=4 | a[4]=false |
| {2} | i=4 | j=1 | k=5 | g[2]=5 |
| {4} | i=4 | j=0 | g[1]=4 |
т. е. g = (4 5 2 1 6 7 3)
|
|
|
Работа алгоритма происходит следующим образом. Подобно алгоритму O1, в каждом цикле первым выбирается элемент с наименьшим значением (переменная i в точке {3}), при этом циклы следуют в порядке возрастания наименьших элементов. За счет рекурсивного вызова процедуры B осуществляется движение по каждому конкретному циклу до его замыкания. При этом глубина рекурсии равна числу элементов цикла. По выходу из каждого очередного уровня рекурсии в массив g заносится текущее значение цикла (точки {2},{4}), при этом массив g заполняется, начиная с больших значений индекса.
Нетрудно видеть, что процедура CANON имеет временную сложность О (n).
Упражнения.
1. Напишите вариант алгоритма CANON без использования рекурсии.
2. Напишите процедуру:
procedure U1(var f: TPE; var g: TPK);
вычисляющую f=g-1×f, если f задана в естественной форме, а g – в канонической.
Наряду с канонической формой циклического разложения перестановки, в которой разметка циклов указывается с помощью левосторонних локальных минимумов, может быть рассмотрена каноническая форма, построенная на левосторонних локальных максимумах; на правосторонних локальных минимумах (максимумах).
Взаимно однозначное соответствие (биекция) между канонической формой циклических разложений и перестановками в естественном представлении позволяет получить ряд интересных фактов. Например, рассмотрим следующий алгоритм поиска индекса минимального элемента в заданном массиве различных вещественных чисел
...
const n =...;
type m = array [1..n] of real;
function INDEX (var a: m): real;
var r: real;
begin r:=a[1]; INDEX:=1;
for i:=2 to n do
if a[i]<r t hen
begin r:=a[i]; INDEX:=i end {1}
end;
...
Возникает естественный вопрос: ‘ Сколько раз в среднем в этом фрагменте программы выполняется оператор {1}, если считать распределения значений элементов в массиве a равновероятным?’.
Заметим, что оператор {1} выполняется только при таких i, когда значение a[i] является левосторонним минимумом, т. е. по теореме 2, оператор {1} выполняется Hn-1 раз.
Упражнение. Оцените среднее число выполнения оператора {1}, если в массиве a допускают равные значения элементов, причем значение индекса должно быть максимально возможным. Как и в примере, считаем, что все возможные распределения значений элементов в a равновероятны.
