Основные формулы. где Х – уровень признака, вариант

Степенная средняя ():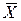

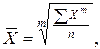
(4.1)

где Х – уровень признака, вариант;

n – число вариантов;

m – показатель степени средней.

Средняя арифметическая ():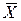

а) простая: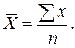

(4.2)

б) взвешенная: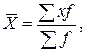

(4.3)

где f – веса (частоты или частости) каждого варианта.

Средняя гармоническая ():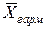

а) простая: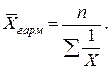

(4.4)

б) взвешенная: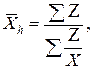

(4.5)

где Z =X*f.

Средняя квадратическая ():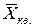

а) простая: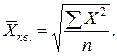

(4.6)

б) взвешенная: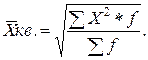

(4.7)

Средняя геометрическая ():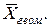

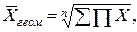
(4.8)

где П – знак произведения.

Расчет средней арифметической «способом моментов» для интервальных рядов распределения:

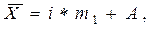
(4.9)

где i – величина интервала;

m₁ – момент первого порядка.

При этом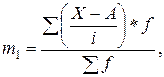

(4.10)

где А – условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой.

Структурные средние для интервальных рядов распределения:

а) мода для интервальных рядов распределения ():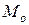

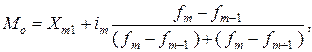
(4.11)

где Х_m – начальное значение интервала, содержащего моду;

i_m – величина модального интервала;

f_m – частота модального интервала;

f_m-1 – частота интервала, предшествующего модальному;

f_m+1 – частота интервала, следующего за модальным.

б) медиана для интервальных рядов распределения ():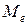

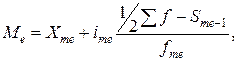
(4.12)

где Х_mе – начальное значение интервала, содержащего медиану;

i_mе – величина медианного интервала;

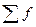– сумма частот ряда;

S_me-1 – кумулятивная частота в интервалах, предшествующих медианному;

f_mе – частота медианного интервала.