2015-01-21
1486
Движение жидкости называется течением, а совокупность частиц движущейся жидкости — потоком. Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис. 45). Линии тока проводятся так, чтобы густота их, характеризуемая отношением числа линий к площади перпендикулярной им площадки, через которую они проходят, была пропорциональна скорости течения жидкости. Таким образом, по картине линий тока можно судить о направлении и модуле скорости течения жидкости в разных точках пространства. Линии тока в жидкости можно «проявить», например, подмешав в нее какие-либо заметные взвешенные частицы.
Часть жидкости, ограниченную линиями тока, называют трубкой тока. Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются.
Рис. 45 Рис.46
Рассмотрим какую-либо трубку тока. Выберем два ее сечения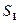 
и 
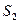, перпендикулярные направлению скорости (рис. 46).
За время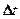 
через сечение 
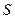проходит объем жидкости 
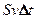; следовательно, за 1 с через 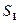пройдет объем жидкости 
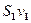, где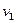 
— скорость течения жидкости в месте сечения 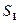. Через сечение 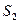за 1 с пройдет объем жидкости 
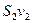, где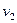 
— скорость течения жидкости в месте сечения 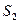. Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема (
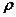= const), то через сечение 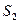пройдет такой же объем жидкости, как и через сечение 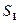, т. е.
(29.1)
Следовательно, произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение (29.1) называется уравнением неразрывности для несжимаемой жидкости.
