2015-01-21
547
Если протекание электрического тока происходит под действием относительно слабого электрического поля, плотность тока линейно зависит от напряжённости поля:
, ()
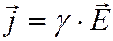где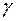 
- удельная проводимость вещества.
Удельная проводимость собственного полупроводника складывается из электронной и дырочной проводимостей, и для плотности тока можно записать:
. ()
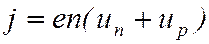В этом выражении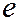 
- заряд электрона или дырки; 
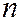- концентрация электронов или дырок; 
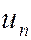и 
- средние скорости их направленного движения.
В относительно слабых полях скорости движения носителей заряда пропорциональны напряженности электрического поля:
, ()
()
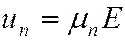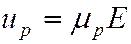Коэффициенты пропорциональности 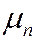и 
и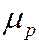 
в называются подвижностями электронов и дырок. Из формул () и () следует, что подвижность носителей заряда – физическая величина, численно равная средней скорости направленного движения носителя при напряжённости электрического поля, равной единице. Для удельной электропроводности можно получить выражение:
. ()
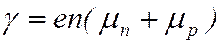Таким образом, удельная электропроводность определяется концентрацией и подвижностью носителей заряда.
Подвижность носителей в собственном полупроводнике определяется их рассеянием на неоднородностях кристаллической решётки и слабо зависит от температуры.
Поэтому, зависимость электропроводности полупроводника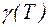 
определится, в основном, зависимостью концентрации носителей от температуры 
.
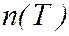Рассмотрим собственный полупроводник. Концентрация носителей в этом случае определится выражением:
, ()
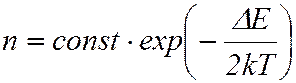и для электропроводности можно записать:
()
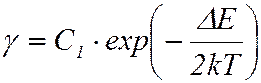Сопротивление полупроводника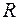 
обратно пропорционально его удельной электропроводности: 
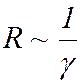, поэтому его зависимость от температуры имеет вид:
. ()
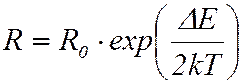Возьмём натуральный логарифм от обеих частей уравнения (), получим:
. ()
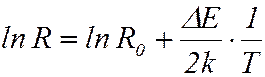Это выражение () представляет собой уравнение прямой линии в координатах: 
; 
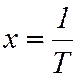. График этой зависимости приведён на рисунке.
Угловой коэффициент этой прямой равен:
. ()
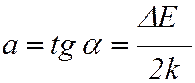Таким образом, из экспериментальной зависимости сопротивления собственного полупроводника от температуры можно определить ширину запрещённой зоны. Для этого необходимо выбрать две точки на прямой (рис.), определить угловой коэффициент по формуле:
, ()
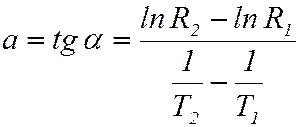а затем ширину запрещённой зоны:
. ()
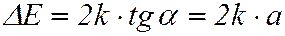Рассмотрим примесный полупроводник (для определённости электронный). В этом случае его электропроводность обусловлена двумя слагаемыми:
. ()
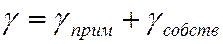Рассмотрим вклад каждого слагаемого в широком диапазоне температур. Учтём, что ΔEd << ΔE.
1. Низкие температуры характеризуются тем, что примесные атомы ионизированы лишь частично, а собственная проводимость ничтожно мала (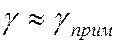
). Тогда концентрация носителей в полупроводнике растёт с температурой по закону:
, ()
и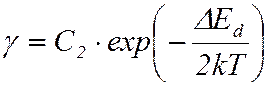 
. ()
2. Средние температуры характеризуются тем, что примесные атомы ионизированы полностью, имеет место примесное истощение, а собственная проводимость ещё мала (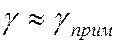). Тогда концентрация носителей в полупроводнике с ростом температуры не изменяется: 
,
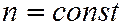и зависимость электропроводности полупроводника от температуры обусловлена зависимостью подвижности носителей заряда 
.
3. Высокие температуры характеризуются тем, что примесные атомы ионизированы полностью, и собственная проводимость преобладает над примесной (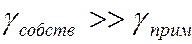
),тогда 
. Концентрация носителей в полупроводнике растёт с температурой по закону:
,
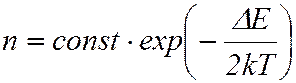и . ()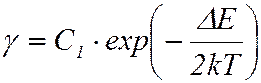
Зависимость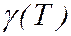 
удобно представлять в координатах: 
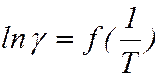; Для примесного полупроводника в широком диапазоне температур график этой зависимости приведён на рисунке.
Участок ab соответствует низким температурам и преобладанию примесной проводимости.
Участок bc соответствует средним температурам и примесному истощению. Проводимость в этой области иногда может уменьшаться, так как с ростом температуры уменьшается подвижность носителей.
Участок cd соответствует высоким температурам и преобладанию собственной проводимости.
Уменьшение электрического сопротивления полупроводника с ростом температуры используется в приборах, называемых термисторами. Эти приборы применяются в схемах для измерения и регулирования температур.
