Первое модельное предположение

Если в регрессионное уравнение включен свободный член, то условие 1 (допущение о равенстве нулю математического ожидания случайной переменной) никогда не нарушается. В тех же случаях, когда возникает необходимость рассмотрения уравнения регрессии с нулевым свободным членом, первое модельное предположение может быть нарушено. Поэтому для устранения проблем с первой предпосылкой в модель регрессии следует включать свободный член.

Выполнение этой предпосылки может быть протестировано разными методами. Один из них заключается в визуальном анализе графика зависимости остатков 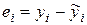результативного признака . Если точки графика разбросаны хаотично по отношению к оси абсцисс, то первая предпосылка выполняется. Если же такой разброс имеет системный характер, то это дает основание для того, чтобы усомниться в выполнимости предпосылки, а следовательно, и в правильности спецификации модели.

Второй подход является статистическим. Как известно, несмещенной оценкой математического ожидания случайной величины является выборочное среднее. Поэтому для проверки предположения о равенстве нулю математического ожидания случайной переменной достаточно оценить величину среднего выборочного остатков регрессии 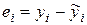, , 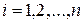т.е. величину .

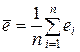Можно также по остаткам 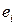с помощью 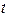-статистики проверить нулевую гипотезу о равенстве нулю математического ожидания случайной переменной 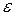(если она распределена по нормальному закону). Для этого сравниваются наблюдаемое значени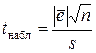е , где 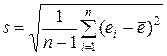– стандартное отклонение, и критическое значение 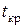статистики Стьюдента с числом степеней свободы, равным 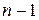. Если 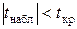, то нулевая гипотеза о равенстве нулю математического ожидания случайной переменной 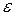принимается, а значит, условие 1 выполняется.