Приближенные числа и их погрешности

В самых разнообразных теоретических и прикладных исследованиях широко используются методы математического моделирования, которые сводят решение задач данной области исследования к решению адекватных (или приближенно адекватных) им математических задач. Необходимо довести решение этих задач до получения числового результата (вычисления различного рода величин, решения различных типов уравнений и т.п.). Целью вычислительной математики является разработка алгоритмов численного решения обширного круга математических задач. Методы должны быть разработаны так, чтобы их можно было эффективно реализовать с помощью современной вычислительной техники. Как правило, рассматриваемые задачи не допускают точного решения, поэтому речь идет о разработке алгоритмов, дающих приближенное решение. Для возможности замены неизвестного точного решения задачи приближенным необходимо, чтобы последнее было достаточно близко к точному. В связи с этим возникает необходимость оценки близости приближенного решения к точному и разработки приближенных методов построения приближенных решений, сколько угодно близких к точным.

Схематически вычислительный процесс заключается в том, чтобы для данной величины x (числовой, векторный и т.д.) вычислить значение некоторой функции A(x). Разность между точным и приближенным значениями величины называют погрешностью. Точное вычисление значения A(x) обычно невозможно, и вынуждает заменить функцию (операцию) A ее приближенным представлением Ã, которое можно вычислить: вычисление величины A(x), заменяется вычислением- Ã(x). Возникающую при этом погрешность A(x) - Ã(x) называют погрешностью метода. Способ оценки этой погрешности должен быть разработан вместе с разработкой метода вычисления величины Ã(x). Из возможных методов построения приближения следует использовать тот, который при имеющихся средствах и возможностях дает наименьшую погрешность.

Значение величины x, то есть исходных данных, в реальных задачах получается или непосредственно из измерений, или в результате предыдущего этапа вычислений. В этих случаях определяется лишь приближенное значение x _o величины x. Поэтому вместо величины Ã(x) может быть вычислено лишь приближенное ее значение Ã(x_o). Возникающую при этом погрешность A(x) - Ã(x_o) называют неустранимой. В результате неизбежных в ходе вычислений округлений, вместо величины Ã(x_o) вычисляется ее «округленное» значение 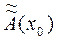, что приводит к появлению погрешности округления Ã(x_o) - 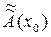. Полная погрешность вычислиниия оказывается равной A(x) - .

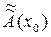Представим полную погрешность в виде

A(x) - 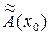= [ A(x) - 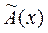] + [ 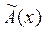- Ã(x_o) ] +

+ [ Ã(x_o) - 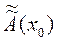] (1)

Последнее равенство показывает, что полная погрешность вычисления равна сумме погрешности метода, неустранимой погрешности и погрешности округления. Первые две составляющие погрешности можно оценить до начала вычислений. Погрешность округления оценивается лишь в ходе вычислений.

Рассмотрим следующие задачи:

а) характеристика точности приближенных чисел

б) оценка точности результата при известной точности исходных данных (оценка неустранимой погрешности)

в) определение необходимой точности исходных данных для обеспечения заданной точности результата

г) согласование точности исходных данных и вычислений с возможностями имеющихся вычислительных средств.