Рассмотрим следующую часто возникающую задачу: значение функции f(x 1 ,x 2 ) вычисляется при приближенных значениях x 01 и x 02 аргументов. Требуется определить, насколько малыми должны быть погрешности ∆x 1и ∆x 2 этих аргументов для того, чтобы неустранимая погрешность вычисления функции не превосходила заданной величины ε > 0.
Это требование можно записать в виде неравенства

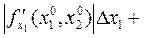
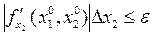
(используя формулу (6')). Таким образом, для определения погрешностей ∆x 1 и ∆x 2 получим одно неравенство с двумя неизвестными, которое имеет бесконечно много решений. Множество решений изображено на рис.3. Любая точка из этого множества дает приемлемые значения погрешностей. Для выделения определенного решения задачи может быть использован принцип равных влияний, согласно которому должны быть разными «вклады» в суммарную погрешность, вызванные неточностями аргументов. Допустимые значения погрешностей определяются из неравенства:
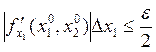 ,
, 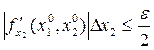
Или, что все равно, из условия:
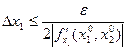 ,
, 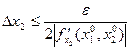 (9)
(9)
Если рассматриваемая функция от нескольких переменных, то в знаменателе вместо двойки появляется число переменных.
Принципом равных влияний разумно пользоваться лишь в случае, когда обеспечение нужной точности определения значений переменных сопряжено с примерно одинаковыми затратами труда. Если же эти затраты существенно различны, то разумнее считать большим «вклад» более трудноизмеримой величины. Считать, например, что он составляет 80-90% от допустимой суммарной погрешности.
Пример 4. Площадь треугольника определяется по двум его сторонам a= 10 см, b=15см и углу 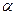 =350 между ними. Определить погрешности измерения указанных величин, при которых абсолютная погрешность площади не превосходит
=350 между ними. Определить погрешности измерения указанных величин, при которых абсолютная погрешность площади не превосходит 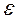 =2см2
=2см2
Начнем с вычисления площади 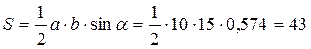 .
.
При определении sin 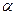 использовались трехзначные таблицы, дающие значения функции с погрешностью ∆т=5 *10-4 . Вызванная этим погрешность метода составляет
использовались трехзначные таблицы, дающие значения функции с погрешностью ∆т=5 *10-4 . Вызванная этим погрешность метода составляет
∆мет=½ *10*15*5*10-4=0.04
Произведенное округление дает погрешность 0.05. Следовательно,
∆мет+∆окр=0.09
и неустранимая погрешность не должна превосходить 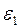 =1.91. Имеем,
=1.91. Имеем, 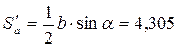 ;
; 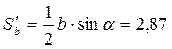 ;
; 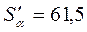
По принципу равных влияний получим:
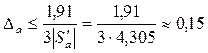 ;
; 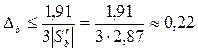 ;
; 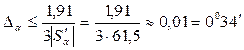
Индивидуальные задания по элементарной теории погрешностей
Задание 1.
Округлить, сохранив в записи лишь три значащие цифры (т.е. три верные цифры, не считая нулей, стоящих слева). Оценить возникающие при этом абсолютную и относительную погрешности.
| Номер варианта | Числа | ||||
| 1. | 0,17452 | 175,5 | 174,5 | ||
| 2. | 425,5 | 424,5 | 3,2978 | 0,17437 | |
| 3. | 123,5 | 124,5 | 4,2983 | 2,74375 | |
| 4. | 0,47153 | 155,5 | 154,5 | 0,75971 | |
| 5. | 244,5 | 245,5 | 1,3971 | ||
| 6. | 7,24375 | 925,5 | 924,5 | 835,71 | 3,9971 |
| 7. | 114,5 | 155,5 | 17,963 | ||
| 8. | 655,5 | 254,5 | 3,1973 | 1024,7 | |
| 9. | 725,53 | 725,5 | 814,5 | 1,5962 | |
| 10. | 815,5 | 0,1845 | 935,52 | 0,18045 | |
| 11. | 105,5 | 114,5 | 355,53 | 0,32961 | |
| 12. | 44,55 | 445,51 | 0,02971 | ||
| 13. | 0,03298 | 24,65 | 3214,5 | ||
| 14. | 33,55 | 34,451 | 6677,1 | ||
| 15. | 0,002955 | 441,2 | 44,652 | ||
| 16. | 325,5 | 33,65 | 14,11 | ||
| 17. | 0,2375 | 33,452 | |||
| 18. | 37,51 | 0,3465 | 444,52 | ||
| 19. | 46,85 | 1,343 | 0,03251 | ||
| 20. | 43,55 | 11,42 | 1465,2 | ||
| 21. | 13,58 | 0,4235 | |||
| 22. | 11,342 | 0,002755 | |||
| 23. | 14,45 | 1,36522 | |||
| 24. | 13,65 | 1,875 | 0,04253 | ||
| 25. | 12,45 | 0,02851 | 1,42501 | ||
| 26. | 0,001251 | 37,55 | 144,501 | ||
| 27. | 13,2503 | 13,25 | 1,435 | ||
| 28. | 14,85 | 0,4981 | |||
| 29. | 42,75 | 1,997 | 0,002921 | ||
| 30. | 0,003857 | 43,451 |
Задание 2.
Заданы приближенные значения аргументов и их абсолютные погрешности. Вычислить приближенное значение функции и оценить абсолютную и относительную погрешности.
| Номер варианта | Функции u(x,y) | x0 | y0 | 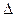 x x
| 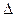 y y
|
| 1 (k=1) | 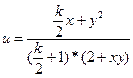
| 0,03 | 0,02 | ||
| 2 (k=2) | |||||
| 3 (k=3) | |||||
| 4 (k=12) | 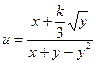
| 0,7 | 0,05 | 0,03 | |
| 5 (k=15) | |||||
| 6 (k=18) | |||||
| 7 (k=21) | 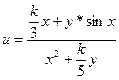
| 0,01 | 0,05 | ||
| 8 (k=24) | |||||
| 9 (k=27) | |||||
| 10 (k=32) | 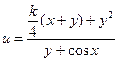
| 0,03 | 0,02 | ||
| 11(k=36) | |||||
| 12(k=40) | |||||
| 13(k=42) | 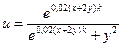
| 0,8 | 0,05 | 0,01 | |
| 14(k=45) | |||||
| 15(k=50) | |||||
| 16(k=52) | 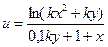
| 0,3 | 0,01 | 0,02 | |
| 17(k=55) | |||||
| 18(k=60) | |||||
| 19(k=64) | 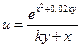
| 0,05 | 0,1 | ||
| 20(k=66) | |||||
| 21(k=70) | |||||
| 22(k=72) | 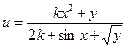
| 1,5 | 0,03 | 0,05 | |
| 23(k=75) | |||||
| 24(k=80) | |||||
| 25(k=84) | 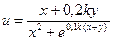
| 0,8 | 0,5 | 0,02 | 0,02 |
| 26(k=86) | |||||
| 27(k=88) | |||||
| 28(k=92) | 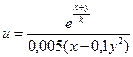
| 0,3 | 0,1 | ||
| 29(k=95) | |||||
| 30(k=100) |
Задание 3.
Используя данные таблицы, найти:
a) значение функции f(x) при заданном значении аргумента x;
b) значение аргумента по заданному значению функции.
Оценить погрешность вычислений.
| Номер варианта | Для пункта a) | Для пункта b) | |
| Функция | Аргумент | Значение функции | |
| 1 (k=1) | cosx | 350+208’k | lnx=-x+0,7k |
| 2 (k=2) | |||
| 3 (k=3) | |||
| 4 (k=12) | tg2x | 150+2013’k | cosx=0,73254+0,01(k-5) |
| 5 (k=15) | |||
| 6 (k=18) | |||
| 7 (k=21) | sinx | 200+107’k | ex=2,37+0,2k |
| 8 (k=24) | |||
| 9 (k=27) | |||
| 10 (k=32) | ctgx | 250+1020’k | sinx=0,25731+0,08(k-10) |
| 11(k=36) | |||
| 12(k=40) | |||
| 13(k=42) | ex | 1,1 +0,005(k-40)2 | ctgx=1,17524+0,1k |
| 14(k=45) | |||
| 15(k=50) | |||
| 16(k=52) | lnx | 25,65+k2/20 | tgx=-5,25731+0,1k |
| 17(k=55) | |||
| 18(k=60) | |||
| 19(k=64) | lgx | 110,25+k/50 | arcsinx=0,625*1/(k-70) |
| 20(k=66) | |||
| 21(k=70) | |||
| 22(k=72) | arctgx | 2,7354+k2/100 | ex=1,75425+0,03k |
| 23(k=75) | |||
| 24(k=80) | |||
| 25(k=84) | arcsinx | 0,8654+0,01(k-80) | lgsinx=-0,8236/(90-k) |
| 26(k=86) | |||
| 27(k=88) | |||
| 28(k=92) | 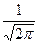 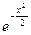
| -1,47+0,01k | arcctgx=1,475/(k-10) |
| 29(k=95) | |||
| 30(k=100) |
 2015-01-21
2015-01-21 580
580








