Формула Симпсона (формула парабол)

Для получения формулы Симпсона коэффициенты Котеса (5) вычисляются при .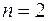

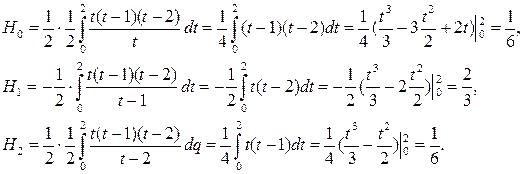(11)

В результате квадратурная формула примет вид

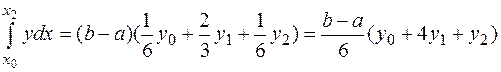(12)

Учитывая, что 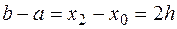получим формулу Симпсона для приближенного интегрирования

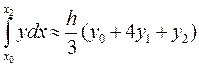(13)

Геометрический смысл формулы Симпсона состоит в том, что в кривая 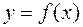заменяется параболой 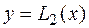, проходящей через три точки .

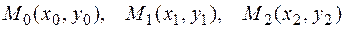Остаточный член формулы Симпсона равен

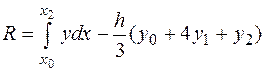
Зафиксируем среднюю точку , и запишем выражение для остаточного члена, как функции от

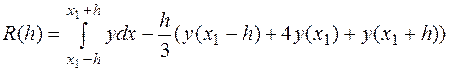(14)

Остаточный член формулы Симпсона равен

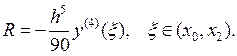(15)

Формула Симпсона имеет повышенную точность для многочленов второй и третьей степени.

Пусть 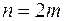есть четное число и 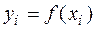значения функции в равноотстоящих точках 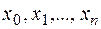с шагом 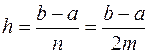. Применяя формулу Симпсона (13) к каждому удвоенному промежутку 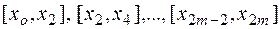длины 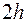получим

.

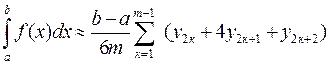После преобразования правой части получим формулу Симпсона в виде удобном для вычислений

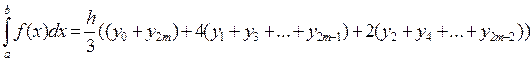(18)

Погрешность вычисления при использовании формулы Симпсона

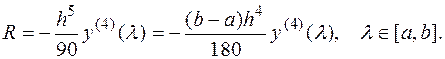
Пример. Вычислить интеграл I= 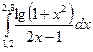по формуле Симпсона при n =10 и оценить погрешность результата с помощью таблицы конечных разностей.

Вычислим шаг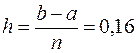

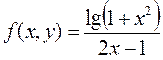- подынтегральная функция.

Значения подынтегральной функции

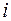
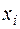
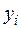
	1,20	0,2767
	1,36	0,2644
	1,52	0,2548
	1,68	0,2468
	1,84	0,2396
	2,00	0,2330
	2,16	0,2269
	2,32	0,2212
	2,48	0,2157
	2,64	0,2106
	2,80	0,2058

Значение интеграла вычисляем по формуле:

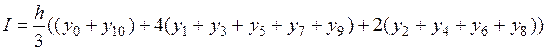
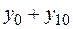
	0,4825
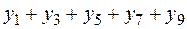
	1,1759
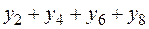
	0,9370
Значение интеграла	0,3765

Для оценки точности полученного результата составим таблицу конечных разностей функции до разностей четвертого порядка

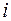
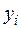
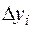
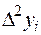
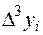
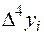
	0,2767	-0,01230	0,00273	-0,00126	0,00068
	0,2644	-0,00957	0,00148	-0,00057	0,00029
	0,2548	-0,00809	0,00090	-0,00028	0,00013
	0,2468	-0,00719	0,00062	-0,00015	0,00006
	0,2396	-0,00657	0,00046	-0,00009	0,00003
	0,2330	-0,00611	0,00038	-0,00005	0,00002
	0,2269	-0,00573	0,00032	-0,00004	0,00001
	0,2212	-0,00541	0,00029	-0,00003
	0,2157	-0,00512	0,00026
	0,2106	-0,00487

Из таблицы следует, что 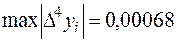, тогда остаточный член, определяющий погрешность вычислений, будет равен

.

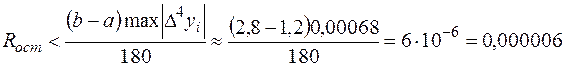Требование к точности вычисления ограничивается четырьмя знаками после запятой, остаточный член на два порядка меньше, следовательно, необходимая точность вычислений достигнута.