Требуется проинтегрировать уравнение 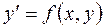 при начальном условии
при начальном условии 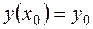 . Одним из разностных методов приближенного решения этой задачи является метод Адамca. Метод позволяет получить решение дифференциального уравнения с заданной точностью
. Одним из разностных методов приближенного решения этой задачи является метод Адамca. Метод позволяет получить решение дифференциального уравнения с заданной точностью 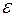 . Алгоритм метода состоит из следующих шагов:
. Алгоритм метода состоит из следующих шагов:
1.Задать некоторый шаг h изменения аргумента и вычислить значения 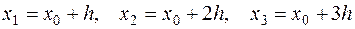
 .
.
2.Вычислить три значения искомой функции 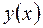 :
:
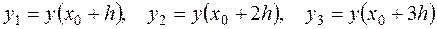 .
.
3.По значениям аргумента и функции вычислить величины
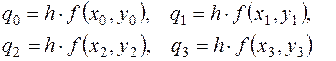 .
.
4. Составить таблицу конечных разностей:
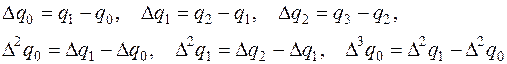 .
.
| x | Y | Δ y | q | Δ q | Δ2 q | Δ3 q |
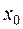 | 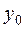 | 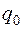 | ||||
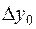 | 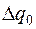 | |||||
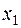 | 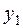 | 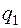 | 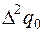 | |||
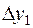 | 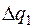 | 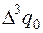 | ||||
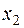 | 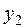 | 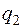 | 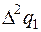 | |||
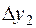 | 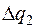 | |||||
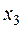 | 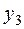 | 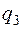 | ||||
| … | … | … | … | … | … | … |
5.По формуле Адамса найти значения
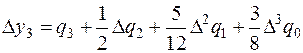 ,
,
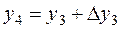 .
.
6.Вычислить 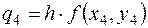 и следующие конечные разности
и следующие конечные разности
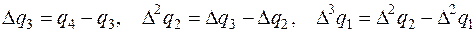 .
.
7. Вычислить
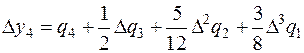 , и затем
, и затем 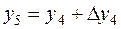 .
.
8. Вычисления продолжаются в соответствии с п.6 и п.7 до достижения необходимой точности.
Пример. Используя метод Адамса со вторыми разностями, составить таблицу приближенных решений дифференциального уравнения 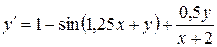 , удовлетворяющего начальному условию
, удовлетворяющего начальному условию 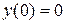 на отрезке
на отрезке 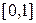 , шаг
, шаг 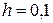 . Все вычисления вести с четырьмя десятичными знаками. Начальный отрезок определить методом Рунге – Кутта.
. Все вычисления вести с четырьмя десятичными знаками. Начальный отрезок определить методом Рунге – Кутта.
Решение. На первом этапе определим начальный отрезок.
Начальное условие дает точку 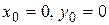 .
.
Следующее значение функции 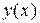 при
при 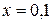 находим методом Рунге-Кутта, результат вычислений в таблице.
находим методом Рунге-Кутта, результат вычислений в таблице.
| x | y | 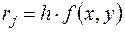 | Добавка |
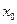 =0 =0 | 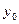 =0 =0 | 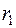 =0,1 =0,1 | 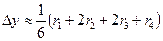 |
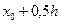 =0,0500 =0,0500 | 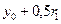 =0,0500 =0,0500 | 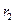 =0,0900 =0,0900 | 0,0908 |
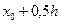 =0,0500 =0,0500 | 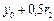 =0,0450 =0,0450 | 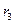 =0,0904 =0,0904 | |
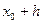 =0,1000 =0,1000 | 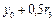 =0,0452 =0,0452 | 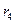 =0,0841 =0,0841 | |
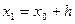 =0,1 =0,1 | 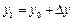 =0,0908 =0,0908 |
Получена вторая точка начального отрезка 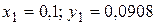
Вычисляем третью точку
| X | Y | 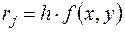 | Добавка |
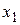 =0,1 =0,1 | 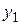 =0,0908 =0,0908 | 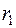 =0,0807 =0,0807 |  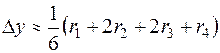 |
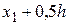 =0,1500 =0,1500 | 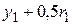 =0,1312 =0,1312 | 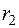 =0,0717 =0,0717 | 0,0724 |
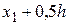 =0,1500 =0,1500 | 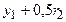 =0,1267 =0,1267 | 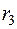 =0,0720 =0,0720 | |
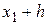 =0,2000 =0,2000 | 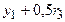 =0,1268 =0,1268 | 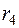 =0,0661 =0,0661 | |
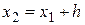 =0,2 =0,2 | 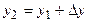 =0,1632 =0,1632 |
Получена третья точка начального отрезка 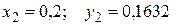
Таким образом, получены точки начального отрезка
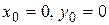
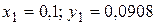
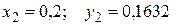
Вычисление следующих значений получим по формуле Адамса со вторыми разностями
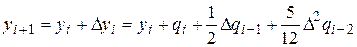 .
.
Конечные разности для точек начального участка вычисляются по формулам:
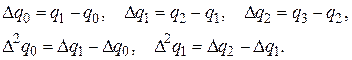
Результаты вычислений занесены в таблицу
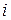 | 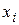 | 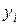 | 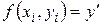 | 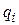 | 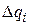 |  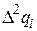 |
| 0,0000 | 1,0000 | 0,1000 | -0,0192 | 0,0020 | ||
| 0,1 | 0,0903 | 0,8079 | 0,0808 | -0,0172 | 0,0024 | |
| 0,2 | 0,1623 | 0,6362 | 0,0636 | -0,0148 | 0,0024 | |
| 0,3 | 0,2181 | 0,4884 | 0,0488 | -0,0124 | 0,0023 | |
| 0,4 | 0,2606 | 0,3649 | 0,0365 | -0,0100 | 0,0022 | |
| 0,5 | 0,2919 | 0,2646 | 0,0265 | -0,0079 | 0,0020 | |
| 0,6 | 0,3144 | 0,1860 | 0,0186 | -0,0059 | 0,0019 | |
| 0,7 | 0,3299 | 0,1273 | 0,0127 | -0,0040 | 0,0018 | |
| 0,8 | 0,3405 | 0,0872 | 0,0087 | -0,0022 | ||
| 0,9 | 0,3480 | 0,0648 | 0,0065 | |||
| 0,3541 |
Индивидуальные задания по приближенным методам решения обыкновенных дифференциальных уравнений (метод рунге-кутта)
Задание 1
1) Используя метод Рунге-Кутта, построить решения предлагаемой ниже задачи Коши на интервале [ k/20, k/20+1 ], где k - номер варианта. Начальный шаг h=0,1.
2) Деля шаг пополам, получить решение с тремя верными знаками после запятой.
| Номер варианта | Уравнение | Начальное условие |
| 1 (k=1) | 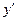 = = 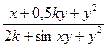 | 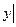 x=0,05k=0,05k x=0,05k=0,05k |
| 2 (k=2) | ||
| 3 (k=3) | ||
| 4 (k=12) | 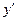 = = 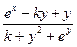 | 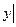 x=0,05k=0,1k x=0,05k=0,1k |
| 5 (k=15) | ||
| 6 (k=18) | ||
| 7 (k=21) | 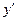 = = 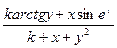 | 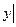 x=0,05k=0,5(k-20) x=0,05k=0,5(k-20) |
| 8 (k=24) | ||
| 9 (k=27) | ||
| 10 (k=32) | 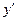 = = 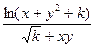 | 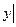 x=0,05k=0,1k x=0,05k=0,1k |
| 11(k=36) | ||
| 12(k=40) | ||
| 13(k=42) | 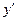 = = 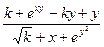 +x +x | 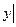 x=0,05k=0,1k x=0,05k=0,1k |
| 14(k=45) | ||
| 15(k=50) | ||
| 16(k=52) | 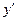 = = 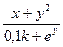 | 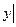 x=0,05k=0,5(k-50) x=0,05k=0,5(k-50) |
| 17(k=55) | ||
| 18(k=60) | ||
| 19(k=64) | 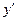 = = 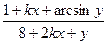 | 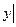 x=0,05k=0,01k x=0,05k=0,01k |
| 20(k=66) | ||
| 21(k=70) | ||
| 22(k=72) | 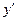 = = 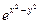 (xy+1- (xy+1- 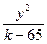 ) ) | 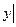 x=0,01k=0,02k x=0,01k=0,02k |
| 23(k=75) | ||
| 24(k=80) | ||
| 25(k=84) | 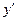 = = 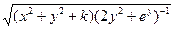 | 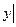 x=0,01k=0,01k x=0,01k=0,01k |
| 26(k=86) | ||
| 27(k=88) | ||
| 28(k=92) | 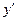 = = 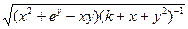 | 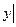 x=0,05k=0,01k x=0,05k=0,01k |
| 29(k=95) | ||
| 30(k=100) |
 2015-01-21
2015-01-21 7527
7527
