1. Определить исходное допустимое решение задачи 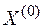 .
.
2. Найти градиент функции в точке исходного допустимого решения 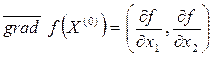 .
.
3. Построить линейную функцию
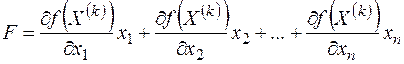 и найти оптимальное решение
и найти оптимальное решение 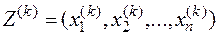 , при котором ее значение максимально при заданных в задаче ограничениях.
, при котором ее значение максимально при заданных в задаче ограничениях.
4. Составить выражение для нового допустимого решения
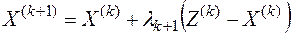 ,
, 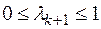
и подставить 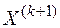 в целевую функцию задачи
в целевую функцию задачи
5. Определить шаг вычислений как стационарную точку функции 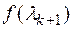 из условия
из условия 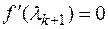 . Полученное значение
. Полученное значение 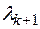 есть шаг вычислений.
есть шаг вычислений.
6. Вычислить новое допустимое решение
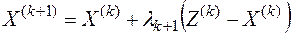 .
.
7. Вычислить значение 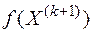 .
.
8. Проверить выполнение условия
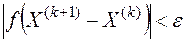 .
.
Если оно выполняется, оптимальное решение найдено, если нет, то переходим к шагу 2.
Пример.
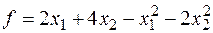
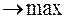
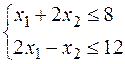
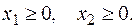
Решение.
1. Найдем градиент функции
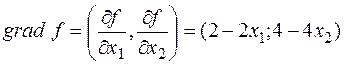 .
.
2. В качестве исходного допустимого решения выберем точку 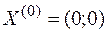 , а в качестве критерия оценки качества получаемого решения неравенство
, а в качестве критерия оценки качества получаемого решения неравенство 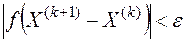 , где
, где 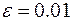 .
.
1-я итерация
1. В точке 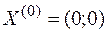 найдем градиент функции
найдем градиент функции 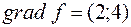 , тогда необходимо решить задачу максимизации
, тогда необходимо решить задачу максимизации
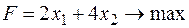 при условии
при условии 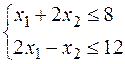
Решаем эту задачу симплекс – методом.
Каноническая задача 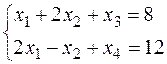
| базис | 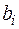 | Q | |||||
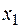 | 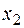 | 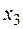 | 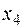 | ||||
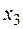 | |||||||
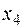 | -1 | ----- | |||||
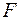 | -2 | -4 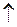 | |||||
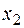 | 1/2 | 1/2 | |||||
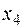 | 5/2 | 1/2 | |||||
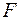 | оптим |
Оптимальное решение 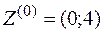
2. Составим новое допустимое решение
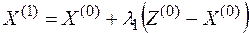 ,
, 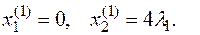
Подставим в целевую функцию, получим
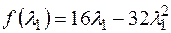 ,
, 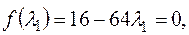
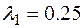
Тогда новое допустимое решение 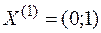 , значение функции в этой точке
, значение функции в этой точке 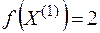 .
.
3. 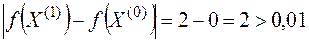 , следовательно, переходим к следующей итерации.
, следовательно, переходим к следующей итерации.
2-ая итерация
1. В точке 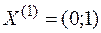 найдем градиент функции
найдем градиент функции 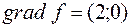 , тогда необходимо решить задачу максимизации
, тогда необходимо решить задачу максимизации
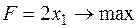 при условии
при условии 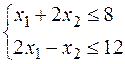
Решаем эту задачу симплекс – методом.
Каноническая задача 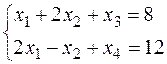
| базис | 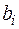 | Q | |||||
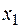 | 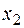 | 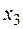 | 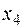 | ||||
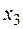 | |||||||
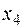 | -1 | ||||||
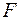 | -2 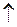 | ||||||
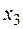 | 5/2 | -1/2 | |||||
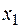 | -1/2 | 1/2 | |||||
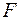 | -1 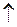 | ||||||
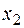 | 4/5 | 2/5 | -1/5 | ||||
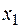 | 32/5 | 1/5 | 2/5 | ||||
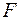 | 64/5 | 2/5 | 4/5 | оптим |
Оптимальное решение 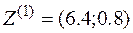
2. Составим новое допустимое решение
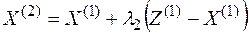 ,
,
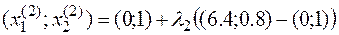
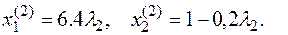
Подставим в целевую функцию, получим
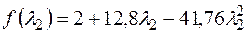 ,
, 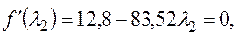
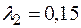
Тогда новое допустимое решение 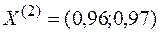 , значение функции в этой точке
, значение функции в этой точке 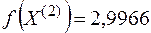 .
.
3. 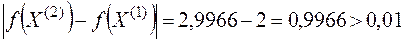 , следовательно, переходим к следующей итерации.
, следовательно, переходим к следующей итерации.
3-я итерация
1. В точке 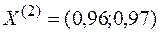 найдем градиент функции
найдем градиент функции 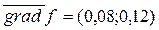 , тогда необходимо решить задачу максимизации
, тогда необходимо решить задачу максимизации
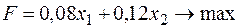 при условии
при условии 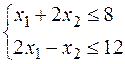
Решаем эту задачу симплекс – методом.
Каноническая задача 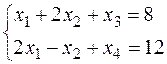
| базис | 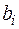 | 0,08 | 0,12 | Q | |||
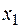 | 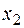 | 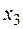 | 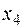 | ||||
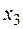 | |||||||
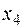 | -1 | ----- | |||||
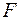 | -0,08 | -0,12  | |||||
| 0,12 | 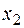 | 1/2 | 1/2 | ||||
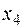 | 5/2 | 1/2 | 32/5 | ||||
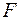 | 0,28 | -0,02  | 0,06 | ||||
| 0,12 | 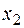 | 4/5 | 2/5 | -1/5 | |||
| 0,08 | 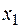 | 32/5 | 1/5 | 2/5 | |||
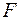 | 0,608 | 0,064 | 0,008 | оптим |
Оптимальное решение 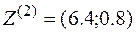
2. Составим новое допустимое решение
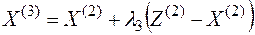 ,
,
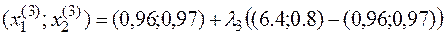
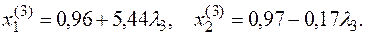
Подставим в целевую функцию, получим
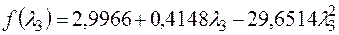 ,
, 
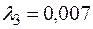
Тогда новое допустимое решение 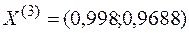 , значение функции в этой точке
, значение функции в этой точке 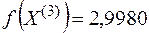 .
.
3. 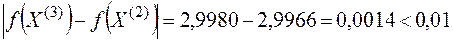 , следовательно, вычисления закончены. Искомое решение
, следовательно, вычисления закончены. Искомое решение 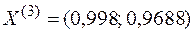 .
.
 2015-01-21
2015-01-21 777
777








