Вопросы к заданию 14

1. Почему метод Симпсона также называют методом парабол?

2. Каким требованиям должно удовлетворять количество интервалов на всем отрезке интегрирования?

3. Какое практическое правило используется для оценки погрешности инте-грирования по методу Симпсона?

4. По результатам сравнения докажите, что метод Симпсона точнее других изученных методов интегрирования. Объясните причину.

ЗАДАНИЕ 15. МЕТОД ЭЙЛЕРА ДЛЯ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

15-1. Используя метод Эйлера, найти численное решение дифференциального уравнения 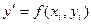, удовлетворяющее начальному условию 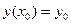. Ограничиться отысканием первых четырех значений 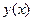с шагом 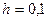. Оценить абсолютную погрешность для каждой узловой точки методом двойного пересчета.

15-2. Используя метод Эйлера, найти численное решение дифференциального уравнения 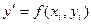, удовлетворяющее начальному условию 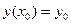. Ограничиться отысканием первых четырех значений 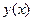с шагом 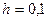. Добиться точности не ниже 0,01, используя метод двойного пересчета (деления шага пополам).

Таблица исходных данных приведена ниже.

Вариант	Уравнение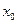
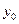
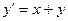
			0,8
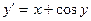
		1,8
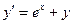
			1,2
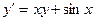
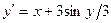
		1,6
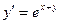
			-1
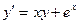
		-1	0,5
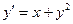
		-2
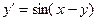
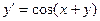
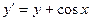
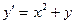
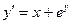
			-1
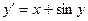
		1,5
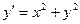
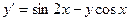
		0,4	0,8
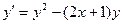
		0,8	1,4
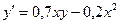
			0,4
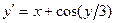
		1,6	4,6
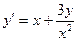
		1,2	2,4
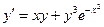
		0,5
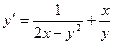
		0,9	1,7
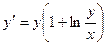
		1,7	5,3
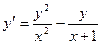
		1,3	2,8
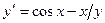
		0,7	2,1
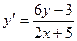
		2,5
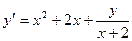
			0,5
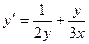
		0,1	0,8
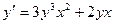
			2,5
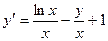
		0,5	2,5
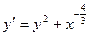
		0,8	1,3
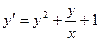
		1,1	1,5
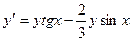
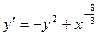
		1,2	2,1
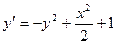
		1,8	2,6