Виды совместимости

1. Понятия А и В называются равнозначными, если объемы этих понятий состоят из одних и тех же элементов.

А, В

Например, понятие "Луна" (А) и "естественный спутник Земли" (В) являются равнозначными.

2. Понятие В подчиняется понятию А, если объем В является собственным подмножеством объема А.

В А

Например, понятие "студент" (В) и "человек" (А); "историк" (В) и "гуманитарий" (А) и т.п.

3. Понятия А и В находятся в отношении перекрещивания, если они совместимы и имеют элементы объема понятия А, не являющиеся элементами объема понятия В, и элементы объема понятия В, не являющиеся элементами объема понятия А.

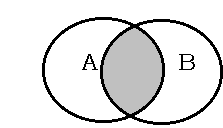
Например, "студент" (А) и "спортсмен" (В); "женщина" (А) и "красивый человек" (В) и др.

Виды несовместимости

1. Понятия А и В называются соподчиненными, если существует третье понятие С, такое, что А подчиняется С и В подчиняется С, и существует элемент объема понятия С, который не входит ни в объем понятия а, ни в объем понятия В.

C

А В

Пример: "студент" (А), "школьник" (В) и "учащийся" (С). Понятия А и В подчиняются понятию С, так как студенты и школьники являются учащимися, но есть еще учащиеся, например, аспиранты, которые не являются ни школьниками, ни студентами.

2. Противоречащими называются понятия А и В, если существует третье понятие С, такое, что А подчиняется С и В подчиняется С и не существует такого элемента объема С, который бы не был элементом объема понятия А или элементом объема понятия В.

С

А В

Пример. Понятия "монархия" (А) и "республика" (В) являются противоречащими понятиями, потому что они не совместимы и оба подчинены понятию С – «форма правления государства", и никакой третьей формы правления нет.

3. Понятия А и В находятся в отношении противоположности, если А и В соподчинены третьему понятию С и представляют собой крайние степени выраженности некоторого качества.

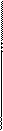С

А В

Пример. Если понятием С будет "цвет", то А – это "белый цвет", а В – "черный цвет"; если С – это понятие "человек", то А – это "мудрец", а В – "глупец".

3.5. Упражнения

1. Среди перечисленных понятий укажите общие, единичные и пустые: журнал «Юность» за декабрь 1989 г.; имя существительное; высшая школа МВД; автор комедии «Ревизор»; круглый квадрат; наименьшее натуральное число; наибольшее натуральное число; участковый инспектор; космический комплекс «Союз-Аполлон»; храбрость; спутник земли; ангел; луноход; столица России.

2. Какие из перечисленных ниже понятий являются:

а) собирательными: число, бригада грузчиков, библиотека, тень, мужество, кооператив, взвод, невежество, деревня, поэзия, свидетель, путешествие, журнал, халатность;

б) абстрактными: деепричастие, отвага, электрон, молния, президент компании, грамотность, стоимость, метро, инициатива, преступность, ускорение, опера.

3. Укажите вид отношения, в котором находятся понятия в каждой из этих пар: 1) слово – имя существительное; 2) понятие – слово; 3) книга – учебник; 4) курсант – учащийся; 5) учитель – мужчина; 6) хирург – терапевт; 7) добросовестность – халатность; 8) Луна – естественный спутник Земли; 9) герой – милиционер; 10) преступление – взятка.

4. Определите отношение между понятиями и изобразите их с помощью круговых схем:

1) населенный пункт, город, станица, деревня, поселок, районный центр;

2) литературное произведение, драма, стихотворение, роман, поэтическое произведение, комедия;

3) мужчина, сын, отец, дедушка;

4) хозяйственное преступление, обман покупателей, незаконное изготовление спиртных напитков;

5) адвокат, юрист, прокурор, следователь, офицер, полковник МВД, капитан I ранга;

6) республика, федеративная республика, государство, монархия, парламетарная монархия;

7) наказуемое деяние, преступление, оскорбление, хулиганство, оскорбление словом, избиение.

5. Определите, соответствуют ли понятия и схемы друг другу?

1). время (А), минута (В), секунда (С), час (Д)

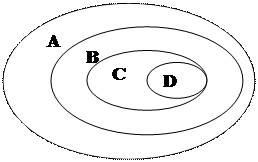2) преступления (А), взятка (В), грабеж (С)

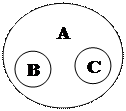3) учебное пособие (А), книга (В), таблица (С), таблица (Д)

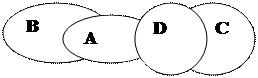4. Рота (А), взвод (В), отделение (С)

5. Автомобиль (А), автомобиль «Жигули» (В), автомобиль «Жигули» синего цвета (С).

6. Свидетель происшествия (А), виновник происшествия (В), водитель автомобиля (С), пешеход (Д)

4. Определение понятий.

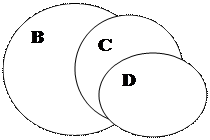Определение – логическая операция, раскрывающая основное содержание понятия путем перечисления входящих в него признаков.

Например, республика- форма правления, при которой все высшие органы государственной власти либо избираются всеобщим голосованием, либо формируется общенациональными представительными учреждениями.

Любое определение: 1. Отличает предметы, входящие в объем данного понятия от всех остальных предметов; 2.раскрывает сущность предмета.

4.1. Виды определений.

1. Номинальные и реальные.

Номинальным называется определение, создающее содержание вновь вводимого понятия.

Например, определение: «Коллективные образования как субъекты гражданского права именуются юридическими лицами» – номинальное, так как здесь впервые вводится смысл термина «юридическое лицо».

Реальным называется определение такого понятия, о содержании и объеме которого мы имеем представление до этого определения.

Реальным является определение Платоном понятия «человек»: «Человек- это животное двуногое и бесперое». Платон перечислил признаки, которые, по его мнению, позволяли отличить человека от всех остальных животных.

2. Явные и неявные.

Явным называется определение, которое имеет форму равенства: А=df B или может быть приведено к ней.

Явное определение имеет структуру:

a) Равенство в целом называется определением, - definitia.

b) Понятие, которое подвергается определению, называется определяемым понятием. В данном случае, это понятие – А – definiendum.

c) Понятие, при помощи которого определяется другое понятие, называется определяющим – понятие В- definiens.

Большая часть определений, которыми занимается логика, относятся к числу явных.

Неявное определение – это определение, которое не имеет формы равенства А = df В, где А –определяемое понятие.

Например, содержание понятий «точка», «прямая», «плоскость» в евклидовой геометрии задается аксиомами этой системы геометрии.

Аксиоматическими называются определения, в которых содержание понятий задается системой аксиом, в которых это понятие встречается.

Другой пример: операция возведения в квадрат в арифметике определяется контекстуально: а²= а х а

Контекстуальным называется определение, в котором некоторый контекст использования определяемого понятия приравнивается к другому контексту, в который определяемое понятие не входит.

Третий вид неявных определений – остенсивные –определение осуществляется путем прямого указания на предмет, входящий в объем данного понятия.

Недостаток их заключается в том, что они не фиксируют значения термина отчетливо.

Например, если ребенок спрашивает нас, что такое лошадь, мы показываем ему лошадь на улице или в цирке и говорим ему: «Это- лошадь».

Остановимся подробнее на явных определениях.

Большинство явных определений принадлежит к числу родовидовых,то есть определений через ближайший род и видовое отличие.

Видовым отличием называется признак, при помощи которого из данного рода выделяется некоторый его вид.

Родовидовым называется определение через род и видовое отличие.

А=df В и С, где А- определяемое понятие, а В и С –определяющее понятие, В- обозначает род, а С- видовое отличие.

Пример: “ Преступление есть предусмотренное уголовным законом общественно опасное деяние”, где роль А играет понятие “преступление”, “В”-деяние, “С”- предусмотренное уголовным законом общественно опасное”.

4.2. Правила определения.