Статистическая теория, в отличие от структурной, позволяет оценивать информационные системы в конкретных условиях их применения, например, при передаче сообщений по каналам связи с шумами.
Статистическая теория оперирует понятием энтропии, введенной американским ученым Шенноном и определяемой выражением:
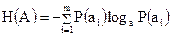 , (1.9)
, (1.9)
где m – число возможных состояний объекта А; 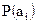 – вероятность нахождения объекта А в i-ом состоянии,
– вероятность нахождения объекта А в i-ом состоянии, 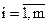 ;
; 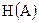 – энтропия объекта А.
– энтропия объекта А.
В (1.9) предполагается, что имеет место ансамбль событий, т.е. полная группа событий (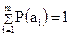 ) с известным распределением вероятностей.
) с известным распределением вероятностей.
Если в (1.9) основание логарифма 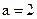 , то единицей измерения энтропии является бит, при
, то единицей измерения энтропии является бит, при 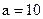 – дит, если логарифм натуральный – нат.
– дит, если логарифм натуральный – нат.
Энтропия 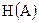 характеризует неопределенность состояния объекта А и использована Шенноном в статистической теории для определения количества информации
характеризует неопределенность состояния объекта А и использована Шенноном в статистической теории для определения количества информации 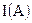 , получаемое об объекте А в результате информационного обмена:
, получаемое об объекте А в результате информационного обмена:
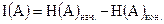 , (1.10)
, (1.10)
где 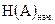 – априорная энтропия объекта А, т.е. неопределенность состояния объекта А, имеющаяся у получателя информации до информационного обмена;
– априорная энтропия объекта А, т.е. неопределенность состояния объекта А, имеющаяся у получателя информации до информационного обмена; 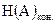 – апостериорная неопределенность объекта А, т.е. остающаяся у получателя после информационного обмена.
– апостериорная неопределенность объекта А, т.е. остающаяся у получателя после информационного обмена.
Единицы измерения 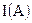 те же, что и для энтропии
те же, что и для энтропии 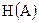 .
.
Априорная энтропия 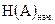 определяется по формуле (1.9) после предварительного анализа объекта А с целью выяснения числа возможных состояний объекта А – m и вероятностей нахождения объекта в этих состояниях –
определяется по формуле (1.9) после предварительного анализа объекта А с целью выяснения числа возможных состояний объекта А – m и вероятностей нахождения объекта в этих состояниях – 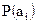 ,
, 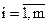 .
.
Для определения апостериорной энтропии 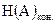 необходимо привлекать понятия объединения и условной энтропии. Рассмотрим эти понятия.
необходимо привлекать понятия объединения и условной энтропии. Рассмотрим эти понятия.
Объединением называется совокупность двух и более ансамблей дискретных случайных переменных. Рассмотрим объединение двух объектов А и В. Пусть число возможных состояний объекта А равно m, а объекта В – n. Возможные состояния объектов обозначим соответственно: 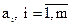 ;
; 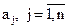 .
.
Результатом объединения явится сложный объект (А, В). Его состояния 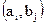 представляют собой всевозможные комбинации состояний объектов А и В. Обозначим вероятность нахождения сложного объекта (А, В) в этих состояниях через
представляют собой всевозможные комбинации состояний объектов А и В. Обозначим вероятность нахождения сложного объекта (А, В) в этих состояниях через 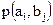 .
.
Из теории вероятностей известно, что для независимых объектов
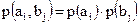 , (1.11)
, (1.11)
а для зависимых объектов
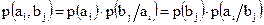 , (1.12)
, (1.12)
где 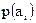 и
и 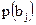 – безусловные вероятности нахождения объектов А и B в соответствующих состояниях, а
– безусловные вероятности нахождения объектов А и B в соответствующих состояниях, а 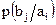 и
и 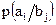 – условные вероятности:
– условные вероятности: 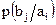 – вероятность того, что объект В примет конкретное состояние
– вероятность того, что объект В примет конкретное состояние 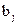 , если объект А принял состояние
, если объект А принял состояние 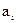 ;
; 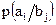 – вероятность того, что объект А примет состояние
– вероятность того, что объект А примет состояние 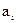 , если объект В принял состояние
, если объект В принял состояние 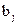 .
.
Предположим, что объект В принял состояние 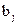 и определим энтропию объекта А при условии, что В находится в этом конкретном состоянии. Такая энтропия называется условной, обозначается
и определим энтропию объекта А при условии, что В находится в этом конкретном состоянии. Такая энтропия называется условной, обозначается 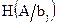 и определяется выражением:
и определяется выражением:
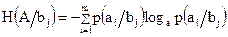 . (1.13)
. (1.13)
Энтропия 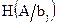 зависит от того, в каком конкретном состоянии находится объект В. Умножив каждую условную энтропию
зависит от того, в каком конкретном состоянии находится объект В. Умножив каждую условную энтропию 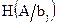 на
на 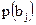 и сложив полученные произведения, получим выражение для средней условной энтропии:
и сложив полученные произведения, получим выражение для средней условной энтропии:
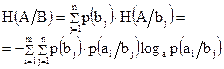 (1.14)
(1.14)
Учитывая (1.12), получаем:
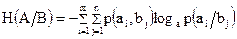 . (1.15)
. (1.15)
По смыслу 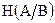 – неопределенность состояния объекта А, остающаяся после того, как состояние объекта В полностью выяснено.
– неопределенность состояния объекта А, остающаяся после того, как состояние объекта В полностью выяснено.
Если отождествить с А передаваемое сообщение о состоянии объекта А, а с В – принимаемое сообщение, тогда средняя условная энтропия 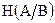 будет характеризовать неопределенность передаваемого сообщения о состоянии объекта А, остающуюся после получения конкретного сообщения, т.е. после выяснения состояния объекта В. По смыслу это соответствует
будет характеризовать неопределенность передаваемого сообщения о состоянии объекта А, остающуюся после получения конкретного сообщения, т.е. после выяснения состояния объекта В. По смыслу это соответствует 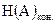 . Итак:
. Итак:
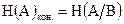 , (1.16)
, (1.16)
а 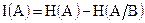 . (1.17)
. (1.17)
Используя полученные результаты, найдем выражения для количества информации, получаемого при передаче сообщений по каналам связи с шумами.
Рассмотрим сначала предельные случаи.
Если помех нет или их уровень настолько низок, что они не в состоянии уничтожить сигнал или имитировать сигнал при отсутствии передачи, то можно быть уверенным, что при передаче сигнала 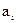 на приемной стороне канала связи будет принят сигнал
на приемной стороне канала связи будет принят сигнал 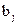 , соответствующий сигналу
, соответствующий сигналу 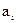 . Между передаваемыми и принимаемыми сигналами в этом случае существует жесткая связь, поэтому
. Между передаваемыми и принимаемыми сигналами в этом случае существует жесткая связь, поэтому 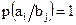 . Условная энтропия
. Условная энтропия 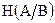 , определяемая выражением (1.15), при этом равна 0, т.к.
, определяемая выражением (1.15), при этом равна 0, т.к. 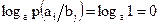 . Количество информации, получаемое в результате информационного обмена,
. Количество информации, получаемое в результате информационного обмена, 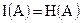 , т.е. максимально возможное.
, т.е. максимально возможное.
При высоком уровне помех статистическая связь между передаваемыми и принимаемыми сообщениями отсутствует, т.е. при передаче любого сигнала 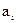 может быть принят любой сигнал
может быть принят любой сигнал 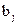 . В этом случае
. В этом случае 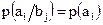 и
и 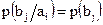 . Условная энтропия
. Условная энтропия 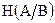 , определяемая (1.15), с учетом (1.12) может быть записана так:
, определяемая (1.15), с учетом (1.12) может быть записана так:
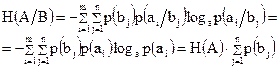
Но 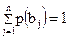 , т.к. состояния объекта В составляют полную группу событий. Следовательно,
, т.к. состояния объекта В составляют полную группу событий. Следовательно, 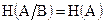 и
и 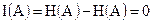 .
.
Информационные характеристики реальных каналов связи лежат между двумя этими предельными случаями. Несмотря на то, что часть информации поражается помехами, статистическая связь между передаваемыми и принимаемыми сообщениями сохраняется. Свойства канала связи при этом задаются канальной матрицей вида 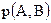 :
:
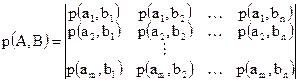 (1.18)
(1.18)
Матрица 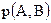 всегда квадратная
всегда квадратная 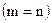 . Вероятности, расположенные по диагонали и соответствующие
. Вероятности, расположенные по диагонали и соответствующие 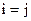 , определяют правильный прием, остальные – ложный.
, определяют правильный прием, остальные – ложный.
Необходимые для расчета 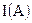 безусловные вероятности
безусловные вероятности 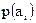 и
и 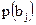 определяются из самой канальной матрицы:
определяются из самой канальной матрицы:
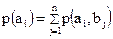 ;
; 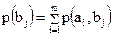 (1.19)
(1.19)
Необходимые для расчета 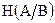 условные вероятности
условные вероятности 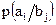 находятся из (1.12) по известным вероятностям
находятся из (1.12) по известным вероятностям 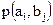 и
и 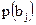 .
.
Матрица 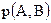 определяется экспериментально и периодически уточняется на основании результатов тестирования канала связи.
определяется экспериментально и периодически уточняется на основании результатов тестирования канала связи.
Выражение (1.17) определяет среднее количество информации, приходящееся на один знак сообщения. Для определения среднего количества информации в сообщении, состоящем из 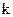 знаков, найденное по (1.17) значение необходимо умножить на
знаков, найденное по (1.17) значение необходимо умножить на 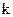 .
.
Кроме отмеченного, при определении 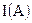 необходимо учитывать статистические свойства источника информации. Осуществляется это следующим образом.
необходимо учитывать статистические свойства источника информации. Осуществляется это следующим образом.
Пусть источник вырабатывает развернутое во времени дискретное сообщение 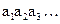 и т.д., где символы при знаках
и т.д., где символы при знаках 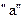 указывают порядок их появления в сообщении. Тогда, если знаки независимы друг от друга, все условные вероятности появления знаков будут равны безусловным:
указывают порядок их появления в сообщении. Тогда, если знаки независимы друг от друга, все условные вероятности появления знаков будут равны безусловным:
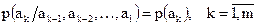 .
.
Если имеется связь только между двумя соседними знаками, то
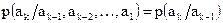 .
.
Корреляция может распространяться и на большее число предшествующих знаков, но у встречающихся на практике источников это число конечно. Такие источники называются эргодическими.
Для эргодических источников может быть найдено конечное число конечных характеристик состояний 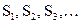 , таких, что условная вероятность появления очередного знака зависит только от того, в каком из этих состояний находился источник до его генерации. Вырабатывая очередной знак, источник переходит из одного состояния в другое или возвращается в исходное. Рассмотрим частные случаи.
, таких, что условная вероятность появления очередного знака зависит только от того, в каком из этих состояний находился источник до его генерации. Вырабатывая очередной знак, источник переходит из одного состояния в другое или возвращается в исходное. Рассмотрим частные случаи.
Если корреляционные связи между знаками отсутствуют, то у источника имеется только одно характерное состояние 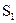 . Вероятность появления знака
. Вероятность появления знака 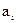 в момент, когда источник находится в этом состоянии, равна
в момент, когда источник находится в этом состоянии, равна 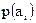 . Выработав знак
. Выработав знак 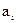 , источник возвращается в исходное состояние
, источник возвращается в исходное состояние 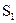 . Энтропия такого источника определяется выражением (1.9).
. Энтропия такого источника определяется выражением (1.9).
Когда корреляция имеется только между соседними знаками, число характерных состояний источника совпадает с объемом используемого алфавита. Находясь в одном из этих состояний, источник, выработав очередной знак, либо возвращается в исходное состояние, либо переходит в другое характерное состояние (номер характерного состояния, в котором окажется источник после генерации очередного знака, совпадает с номером этого знака). Для описания такого источника нужно знать условные вероятности появления знаков 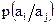 для всех
для всех 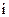 и
и 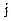 . Найдем энтропию такого источника. Обозначим через
. Найдем энтропию такого источника. Обозначим через 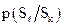 вероятность того, что источник, находясь в состоянии
вероятность того, что источник, находясь в состоянии 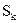 , после генерации очередного знака перейдет в состояние
, после генерации очередного знака перейдет в состояние 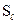 . Тога энтропия источника в
. Тога энтропия источника в 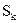 состоянии будет равна:
состоянии будет равна:
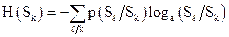 . (1.20)
. (1.20)
Суммирование в (1.20) осуществляется по всем возможным переходам из 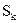 состояния в
состояния в 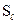 .
.
Умножив 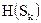 на вероятность нахождения источника в
на вероятность нахождения источника в 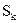 состоянии –
состоянии – 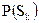 и сложив полученные произведения, получим выражение для средней энтропии источника при наличии корреляции между соседними знаками:
и сложив полученные произведения, получим выражение для средней энтропии источника при наличии корреляции между соседними знаками:
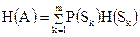 , (1.21)
, (1.21)
где 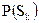 определяется как среднее значение вероятностей генерации знака
определяется как среднее значение вероятностей генерации знака 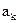 , определенное по всем характерным состояниям источника.
, определенное по всем характерным состояниям источника.
 2015-01-21
2015-01-21 704
704








