Квантование сигналов по времени и по уровню используется при переходе от аналогового представления сигнала к цифровому, что дает значительные преимущества при передаче, хранении и обработке информации.
Для выяснения сущности процессов квантования рассмотрим разновидности функций 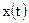 , используемых при описании реальных сигналов.
, используемых при описании реальных сигналов.
| 1. | 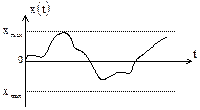
| Непрерывная функция непрерывного аргумента.
Функция 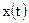 может измениться в любой момент времени на интервале своего существования и принять любое значение из области своего изменения может измениться в любой момент времени на интервале своего существования и принять любое значение из области своего изменения 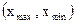 . .
|
| 2. | 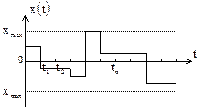
| Непрерывная функция дискрет- ного аргумента.
Функция 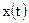 может изменяться только в строго определенные моменты времени, но принимает при этом любые значения из области своего изменения может изменяться только в строго определенные моменты времени, но принимает при этом любые значения из области своего изменения 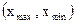 . .
|
| 3. | 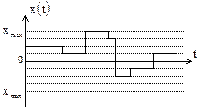
| Дискретная функция непрерывного аргумента.
В данном случае вся область изменения функции 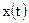 разбита на ряд дискретных уровней, которые может принимать функция в любой момент времени. разбита на ряд дискретных уровней, которые может принимать функция в любой момент времени.
|
| 4. | 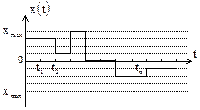
| Дискретная функция дискретного аргумента.
Здесь как значения, которые может принимать функция 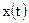 , так и моменты времени, когда происходят ее изменения, являются дискретными. , так и моменты времени, когда происходят ее изменения, являются дискретными.
|
Сигналы, описываемые функциями 1-го типа, называются непрерывными (аналоговыми); 2-го и 3-го типов – дискретно-непрерывными; 4-го типа – дискретными.
Операцию, переводящую непрерывный сигнал во вторую разновидность, называют квантованием по времени или дискретизацией.
Операцию, переводящую непрерывный сигнал в третью разновидность, называют квантованием по уровню.
Совместное применение операций дискретизации и квантования по уровню позволяет преобразовать непрерывный сигнал 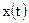 в дискретный по координатам
в дискретный по координатам 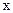 и
и 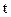 , т.е. перевести его в четвертую разновидность.
, т.е. перевести его в четвертую разновидность.
 2015-01-21
2015-01-21 425
425








