Избыточность сообщений

Энтропия 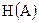, определяемая выражением (1.9), характеризует среднее количество информации, приходящееся на один знак дискретного сообщения, и является максимальной, когда все знаки сообщения равновероятны и независимы друг от друга. При учете вероятностей появления отдельных знаков сообщения, а также статистических связей между знаками, энтропия уменьшается. Это значит, что при наличии связей между знаками часть информации не является непредвиденной для получателя и ее можно было бы не передавать по каналу связи, а восстанавливать на приемной стороне на основании известной связи между знаками. Таким образом, появляется возможность передачи сообщений в сокращенном виде.

Величина, показывающая, какая часть сообщения при данных условиях может быть устранена без потери информации, называется избыточностью.

Абсолютная величина избыточности определяется выражением:

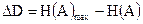, (2.4)

где 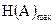– максимальная энтропия сообщения, определяемая при равновероятных и статистически независимых знаках в сообщении; 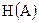– реальная энтропия сообщения.

Относительная избыточность, называемая информационной, определяется выражением:

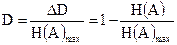. (2.5)

Информационная избыточность показывает относительную недогруженность одного знака алфавита и является безразмерной величиной, изменяющейся в пределах: .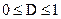

В соответствии с (2.5), избыточность, обусловленная неравновероятным появлением знаков в сообщении, будет равна:

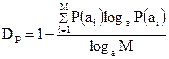, (2.6)

где 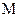– объем используемого алфавита; .

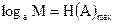Избыточность, вызванная статистической связью между знаками сообщения:

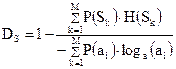, (2.7)

где 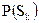– вероятность нахождения источника в 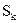характерном состоянии; 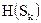– энтропия источника в 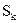состоянии, определяемая выражением (1.20).

Полная информационная избыточность равна [8]:

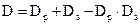(2.8)

Подставляя (2.6) и (2.7) в (2.8), после преобразований, получаем:

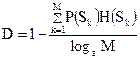(2.9)

Статистический анализ текстов на русском языке показывает, что 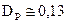, , 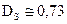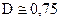. Из этих данных следует, что основная избыточность здесь обусловлена наличием статистической связи между буквами.