2014-01-25
783
УСЛОВИЯ РАВНОВЕСИЯ. УСЛОВИЯ РАВНОВЕСИЯ В ОБЩЕМ И ЧАСТНЫХ СЛУЧАЯХ
Леммой называют теорему, необходимую только для доказательства другой теоремы.
Лемма. Любая система сил эквивалентна системе из двух сил, то есть любая система сил с помощью элементарных операций может быть приведена к двум силам.
Доказательство.
 |
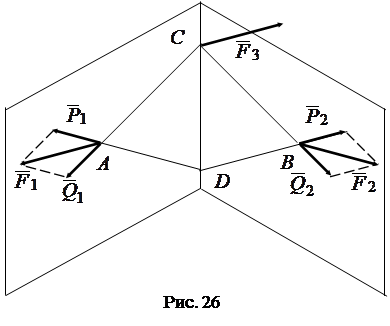Предварительно докажем лемму для трех сил
, 
, 
.
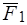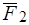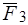Проведем две плоскости (рис. 26); одну через силу 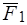и точку 
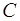, вторую через силу 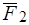и ту же точку .
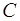Эти плоскости, имея общую точку 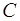, имеют общую прямую. На этой прямой выберем произвольную точку 
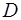и соединим точк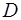и и 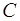прямыми с точкам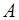и 
и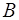 
, в которых приложены силы 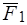и 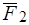. Разложим силы 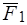и 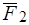на составляющие по проведенным направлениям: 
,
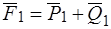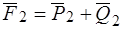. Перенесем силы 
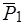и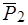 
по их линиям действия в точку 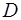, а силы 
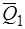и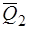 
в точку 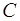(рис. 27). В результате получим две системы сходящихся сил:{
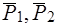} и {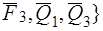
.
 |
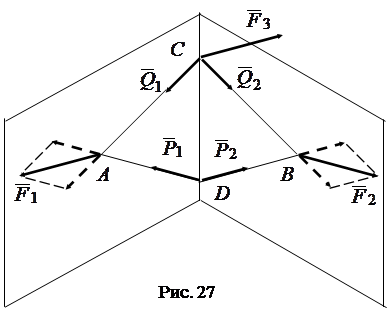Заменяем силы
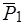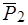и , приложенные в точке 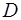, их геометрической суммой 
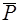, приложенной в той же точке: 
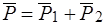, а силы 
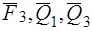, приложенные в точке 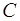– силой 
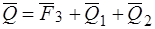, приложенной так же в точке 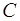. В результате применения только элементарных операций система сил {
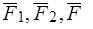} приведена к двум силам {
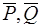}. Итак, заданная система сил {
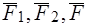} эквивалентна двум силам {}:|
|
|
{}~{},
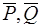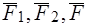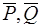что и требовалось доказать.
Если задана система, состоящая из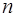 
сил, то тогда, последовательно заменяя каждые три силы двумя, уменьшаем число сил системы. Процесс заканчивается, когда остается только три силы.
{
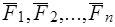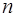} — сил
{
} 
—сил
{
} 
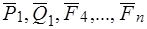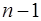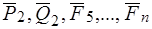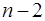—сил
…… …
{} 
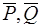—силы
